Exam 7: Multivariate Models
Exam 1: Introduction12 Questions
Exam 2: Mathematical and Statistical Foundations9 Questions
Exam 3: A Brief Overview of the Classical Linear Regression Model28 Questions
Exam 4: Further Development and Analysis of the Classical Linear Regression Model25 Questions
Exam 5: Classical Linear Regression Model Assumptions and Diagnostic Tests20 Questions
Exam 6: Univariate Time Series Modelling and Forecasting29 Questions
Exam 7: Multivariate Models30 Questions
Exam 8: Modelling Long-Run Relationships in Finance18 Questions
Exam 9: Modelling Volatility and Correlation22 Questions
Exam 10: Switching Models19 Questions
Exam 11: Panel Data and Limited Dependent Variable Models12 Questions
Select questions type
Use the following to answer questions
A researcher is interested in forecasting the house price index in Country Z. The observed price index values from 1996 to 2000 are 101, 103 104, 107 and 111. The researcher uses two different forecasting models, A and B. The forecasts for the price index using Model A are 100.5, 102.4, 103.2, 106 and 111 whilst the forecast using Model B are 100.8, 102.2, 104, 104.2 and 112.1.
-What are the closest to the mean squared errors for model A and B's forecasts?
Free
(Multiple Choice)
4.7/5  (34)
(34)
Correct Answer:
C
Which autocorrelation coefficients are significantly different from zero at the 5% level?
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
C
A model where the current value of a variable depends upon only the values that the variable took in previous periods plus an error term is called
Free
(Multiple Choice)
4.8/5  (43)
(43)
Correct Answer:
A
A process, xt, which has a constant mean and variance, and zero autocovariance for all non-zero lags is best described as
(Multiple Choice)
4.8/5  (36)
(36)
The acf is clearly declining very slowly in this case, which is consistent with their being an autoregressive part to the appropriate model. The pacf is clearly significant for lags one and two, but the question is does it them become insignificant for lags 2 and 4, indicating an AR(2) process, or does it remain significant, which would be more consistent with a mixed ARMA process? Well, given the huge size of the sample that gave rise to this acf and pacf, even a pacf value of 0.001 would still be statistically significant. Thus an ARMA process is the most likely candidate, although note that it would not be possible to tell from the acf and pacf which model from the ARMA family was more appropriate. The DGP for the data that generated this plot was y_t = 0.9 y_(t-1) - 0.3 u_(t-1) + u_t.
-Consider the following AR(2) model. What is the optimal 2-step ahead forecast for y if all information available is up to and including time t, if the values of y at time t, t-1 and t-2 are -0.3, 0.4 and -0.1 respectively, and the value of u at time t-1 is 0.3? yt = -0.1 + 0.75yt-1 - 0.125yt-2 + ut
(Multiple Choice)
4.9/5  (33)
(33)
Three characteristics of a weakly stationary process are
(I) 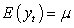 (II)
(II) 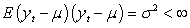 (III)
(III) 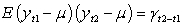
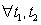 What do the mathematical expressions I, II and III imply?
What do the mathematical expressions I, II and III imply?
(Multiple Choice)
4.9/5  (37)
(37)
Use the following to answer questions
A researcher is interested in forecasting the house price index in Country Z. The observed price index values from 1996 to 2000 are 101, 103 104, 107 and 111. The researcher uses two different forecasting models, A and B. The forecasts for the price index using Model A are 100.5, 102.4, 103.2, 106 and 111 whilst the forecast using Model B are 100.8, 102.2, 104, 104.2 and 112.1.
-What are the closest to the mean absolute errors from models A and B?
(Multiple Choice)
4.9/5  (34)
(34)
Which of the following sets of characteristics would usually best describe an autoregressive process of order 3 )?
(Multiple Choice)
4.9/5  (40)
(40)
Which of these is not a consequence of working with non-stationarity variables?
(Multiple Choice)
4.8/5  (45)
(45)
Which of the following conditions must hold for the autoregressive part of an ARMA model to be stationary?
(Multiple Choice)
4.9/5  (41)
(41)
Consider the following model estimated for a time series yt = 0.3 + 0.5 yt-1 - 0.4 t-1 + t
Where t is a zero mean error process.
What is the (unconditional) mean of the series, yt ?
(Multiple Choice)
4.8/5  (33)
(33)
Consider the following picture and suggest the model from the following list that best characterises the process: 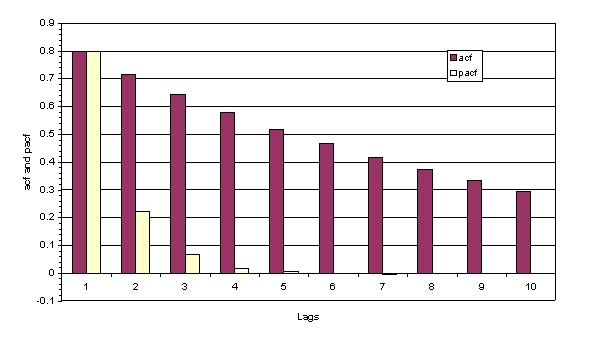
(Multiple Choice)
4.7/5  (42)
(42)
The acf is clearly declining very slowly in this case, which is consistent with their being an autoregressive part to the appropriate model. The pacf is clearly significant for lags one and two, but the question is does it them become insignificant for lags 2 and 4, indicating an AR(2) process, or does it remain significant, which would be more consistent with a mixed ARMA process? Well, given the huge size of the sample that gave rise to this acf and pacf, even a pacf value of 0.001 would still be statistically significant. Thus an ARMA process is the most likely candidate, although note that it would not be possible to tell from the acf and pacf which model from the ARMA family was more appropriate. The DGP for the data that generated this plot was y_t = 0.9 y_(t-1) - 0.3 u_(t-1) + u_t.
-Which of the following models can be estimated using ordinary least squares? (i) An AR(1)
(ii) An ARMA(2,0)
(iii) An MA(1)
(iv) An ARMA(1,1)
(Multiple Choice)
4.7/5  (31)
(31)
If a series, yt, follows a random walk (with no drift), what is the optimal 1-step ahead forecast for y?
(Multiple Choice)
4.9/5  (45)
(45)
The acf is clearly declining very slowly in this case, which is consistent with their being an autoregressive part to the appropriate model. The pacf is clearly significant for lags one and two, but the question is does it them become insignificant for lags 2 and 4, indicating an AR(2) process, or does it remain significant, which would be more consistent with a mixed ARMA process? Well, given the huge size of the sample that gave rise to this acf and pacf, even a pacf value of 0.001 would still be statistically significant. Thus an ARMA process is the most likely candidate, although note that it would not be possible to tell from the acf and pacf which model from the ARMA family was more appropriate. The DGP for the data that generated this plot was y_t = 0.9 y_(t-1) - 0.3 u_(t-1) + u_t.
-What is the optimal three-step ahead forecast from the AR(2) model given in question 14?
(Multiple Choice)
4.9/5  (40)
(40)
Consider the following MA(2) process where the errors follow a standard normal distribution. What is the variance of? 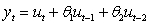
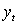
(Multiple Choice)
4.9/5  (33)
(33)
Which of the following statements are true concerning time-series forecasting?
(I) All time-series forecasting methods are essentially extrapolative.
(ii) Forecasting models are prone to perform poorly following a structural break in a series.
(iii) Forecasting accuracy often declines with prediction horizon.
(iv) The mean squared errors of forecasts are usually very highly correlated with the profitability of employing those forecasts in a trading strategy.
(Multiple Choice)
4.8/5  (35)
(35)
Showing 1 - 20 of 30
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)