Exam 2: Introduction to Optimization and Linear Programming
Exam 1: Introduction to Modeling and Decision Analysis52 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet88 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling72 Questions
Exam 6: Integer Linear Programming72 Questions
Exam 7: Goal Programming and Multiple Objective Optimization59 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization68 Questions
Exam 9: Regression Analysis76 Questions
Exam 10: Discriminant Analysis57 Questions
Exam 11: Time Series Forecasting111 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory79 Questions
Exam 14: Decision Analysis102 Questions
Exam 15: Project Management Online61 Questions
Select questions type
Solve the following LP problem graphically by enumerating the corner points.
MAX: 2+7 Subject to: 5+9\leq90 9+8\leq144 \leq8 ,\geq0
(Short Answer)
4.9/5  (35)
(35)
When the objective function can increase without ever contacting a constraint the LP model is said to be
(Multiple Choice)
5.0/5  (34)
(34)
The following diagram shows the constraints for a LP model. Assume the point (0,0) satisfies constraint (B,J) but does not satisfy constraints (D,H) or (C,I). Which set of points on this diagram defines the feasible solution space? 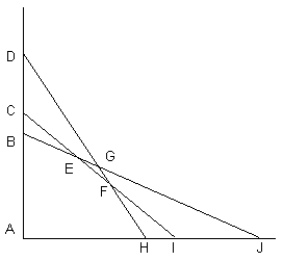
(Multiple Choice)
4.9/5  (37)
(37)
Solve the following LP problem graphically by enumerating the corner points.
MAX: 4+3 Subject to: 6+7\leq84 \leq10 \leq8 ,\geq0
(Short Answer)
4.8/5  (41)
(41)
Most individuals manage their individual retirement accounts (IRAs) so they
(Multiple Choice)
4.8/5  (36)
(36)
Solve the following LP problem graphically using level curves.
MAX: 5+6 Subject to: 3+8\leq48 12+11\leq132 2+3\leq24 ,\geq0
(Short Answer)
4.8/5  (30)
(30)
The following linear programming problem has been written to plan the production of two products. The company wants to maximize its profits. X1 = number of product 1 produced in each batch
X2 = number of product 2 produced in each batch
MAX: 150+250 Subject to: 2+5\leq200 3+7\leq175 ,\geq0 How much profit is earned if the company produces 10 units of product 1 and 5 units of product 2?
(Multiple Choice)
4.8/5  (37)
(37)
The objective function for a LP model is 3 X1 + 2 X2. If X1 = 20 and X2 = 30, what is the value of the objective function?
(Multiple Choice)
4.8/5  (33)
(33)
The second step in formulating a linear programming problem is
(Multiple Choice)
4.9/5  (34)
(34)
Solve the following LP problem graphically using level curves.
MAX: 7+4 Subject to: 2+\leq16 +\leq10 2+5\leq40 \geq0
(Short Answer)
4.9/5  (28)
(28)
A mathematical programming application employed by a shipping company is most likely
(Multiple Choice)
4.9/5  (19)
(19)
Solve the following LP problem graphically by enumerating the corner points.
MIN:
Subject to:
8+5\geq80 3+5\geq60 ,\geq0
(Short Answer)
4.9/5  (31)
(31)
If there is no way to simultaneously satisfy all the constraints in an LP model the problem is said to be
(Multiple Choice)
4.9/5  (36)
(36)
This graph shows the feasible region (defined by points ACDEF) and objective function level curve (BG) for a maximization problem. Which point corresponds to the optimal solution to the problem? 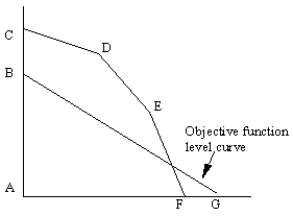
(Multiple Choice)
4.8/5  (28)
(28)
Which of the following actions would expand the feasible region of an LP model?
(Multiple Choice)
4.9/5  (39)
(39)
The following linear programming problem has been written to plan the production of two products. The company wants to maximize its profits. X1 = number of product 1 produced in each batch
X2 = number of product 2 produced in each batch
MAX: 150+250 Subject to: 2+5\leq200 3+7\leq175 ,\geq0 How much profit is earned per each unit of product 2 produced?
(Multiple Choice)
4.9/5  (44)
(44)
Bob and Dora Sweet wish to start investing $1,000 each month. The Sweets are looking at five investment plans and wish to maximize their expected return each month. Assume interest rates remain fixed and once their investment plan is selected they do not change their mind. The investment plans offered are:
Fidelity return per year
Optima return per year
CaseWay return per year
Safeway return per year
National return per year Since Optima and National are riskier, the Sweets want a limit of 30% per month of their total investments placed in these two investments. Since Safeway and Fidelity are low risk, they want at least 40% of their investment total placed in these investments.
Formulate the LP model for this problem.
(Essay)
4.7/5  (35)
(35)
Showing 41 - 60 of 62
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)