Exam 6: Integer Linear Programming
Exam 1: Introduction to Modeling and Decision Analysis52 Questions
Exam 2: Introduction to Optimization and Linear Programming62 Questions
Exam 3: Modeling and Solving Lp Problems in a Spreadsheet88 Questions
Exam 4: Sensitivity Analysis and the Simplex Method72 Questions
Exam 5: Network Modeling72 Questions
Exam 6: Integer Linear Programming72 Questions
Exam 7: Goal Programming and Multiple Objective Optimization59 Questions
Exam 8: Nonlinear Programming and Evolutionary Optimization68 Questions
Exam 9: Regression Analysis76 Questions
Exam 10: Discriminant Analysis57 Questions
Exam 11: Time Series Forecasting111 Questions
Exam 12: Introduction to Simulation Using Risk Solver Platform65 Questions
Exam 13: Queuing Theory79 Questions
Exam 14: Decision Analysis102 Questions
Exam 15: Project Management Online61 Questions
Select questions type
A company is developing its weekly production plan. The company produces two products, A and B, which are processed in two departments. Setting up each batch of A requires $60 of labor while setting up a batch of B costs $80. Each unit of A generates a profit of $17 while a unit of B earns a profit of $21. The company can sell all the units it produces. The data for the problem are summarized below.
Operation A B Hours Cutting 3 4 48 Welding 2 1 36
The decision variables are defined as
Xi = the amount of product i produced
Yi = 1 if Xi > 0 and 0 if Xi = 0
Which of the following constraints creates the link between setting up to produce A's and making some A's for this problem?
(Multiple Choice)
4.8/5  (36)
(36)
An investor has $500,000 to invest and wants to maximize the money they will receive at the end of one year. They can invest in condos, apartments and houses. The profit after one year, the cost and the number of units available are shown below.
Profit Cost Number Variable Investment (\ 1,000) (\ 1,000) Available Condos 6 50 10 Apartments 12 90 5 Houses 9 100 7
Based on this ILP formulation of the problem what formulas should go in cells E5:E12 of the following Excel spreadsheet?
MAX:
Subject ta:
50+90+100\leq500 \leq10 \leq5 \leq7 \geq0 and integer 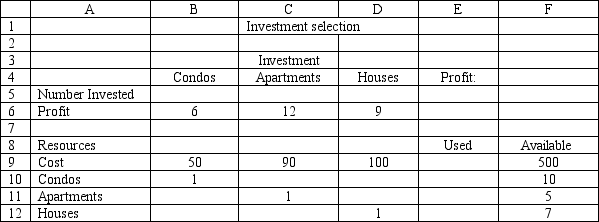
(Essay)
4.8/5  (37)
(37)
Exhibit 6.2
The following questions pertain to the problem, formulation, and spreadsheet implementation below.
A certain military deployment requires supplies delivered to four locations. These deliveries come from one of three ports. Logistics planners wish to deliver the supplies in an efficient manner, in this case by minimizing total ton-miles. The port-destination data, along with destination demand is provided in the following table.
Destination 1 2 3 4 75 88 103 56 105 76 101 85 43 80 95 62 Demand 500 600 450 700
The ports are supplied by one of two supply ships. These ships travel to a particular port where their supplies are off-loaded and shipped to the requesting destinations. Ship S1 carries 1200 tones of supplies while Ship S2 carries 1120 tons of supplies. These ships can only go to a single port and each port can only accommodate one ship. Assume the costs for a ship to travel to a port are not part of the objective function.
The following is the ILP formulation and a spreadsheet model for the problem.
be 1 if ship 1 travels to port , for and be the tons shipped from poit to Destination , D4
Minimize 75+88+103+56+105+76+101+85+43 +80+95+62
Subject to:
+\leq1 +\leq1 +\leq1 ++=1 ++=1 +++\leq1200+1120 +++\leq1200+1120 +++\leq1200+1120 ++\geq500 ++\geq600 ++\geq450 ++\geq700 \geq0
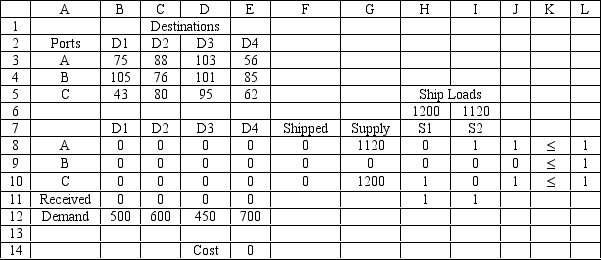 -Refer to Exhibit 6.2. What formula would go into cells B11:E11 and cells F8:F10?
-Refer to Exhibit 6.2. What formula would go into cells B11:E11 and cells F8:F10?
(Essay)
4.7/5  (34)
(34)
A company wants to build a new factory in either Atlanta or Columbia. It is also considering building a warehouse in whichever city is selected for the new factory. The following table shows the net present value (NPV) and cost of each facility. The company wants to maximize the net present value of its facilities, but it only has $16 million to invest.
Variable Decision NPV ( \ millon ) Cost ( \ millon ) Factory in Columbia 3 10 Factory in Atlanta 4 8 Warehouse in Columbia 2 6 Warehouse in Atlanta 1 5 Based on this ILP formulation of the problem what is the optimal solution to the problem?
MAX: 3+4+2+ Subject to: 10++6+5\leq15 +=1 +\leq1 -\leq0 -\leq0 =0,1
(Essay)
4.9/5  (33)
(33)
A small town wants to build some new recreational facilities. The proposed facilities include a swimming pool, recreation center, basketball court and baseball field. The town council wants to provide the facilities which will be used by the most people, but faces budget and land limitations. The town has $400,000 and 14 acres of land. The pool requires locker facilities which would be in the recreation center, so if the swimming pool is built the recreation center must also be built. Also the council has only enough flat land to build the basketball court or the baseball field. The daily usage and cost of the facilities (in $1,000) are shown below.
Formulate the ILP for this problem.
Variable Facility Usage Cost ( \1 ,000) Land Swimming pool 400 100 2 Recreation center 500 200 3 Basketball caut 300 150 4 Baseball Eield 200 100 5
(Essay)
4.8/5  (40)
(40)
A cellular phone company wants to locate two new communications towers to cover 4 regions. The company wants to minimize the cost of installing the two towers. The regions that can be covered by each tower site are indicated by a 1 in the following table:
Region 1 2 3 4 A 1 1 B 1 1 1 C 1 1 1 D 1 1 COST (\ 000) 200 150 190 250
+\geq1 ++\geq1 ++\geq1 +\geq1 +++=2 =0,1 Based on this ILP formulation of the problem and the solution (X1, X2, X3, X4) = (1, 1, 0, 0) what values should go in cells B6:G14 of the following Excel spreadsheet?
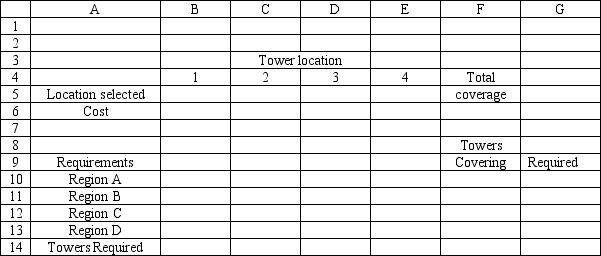
(Essay)
4.7/5  (27)
(27)
If a company selects Project 1 then it must also select either Project 2 or Project 3. Which of the following constraints enforces this condition?
(Multiple Choice)
4.8/5  (33)
(33)
A company is developing its weekly production plan. The company produces two products, A and B, which are processed in two departments. Setting up each batch of A requires $60 of labor while setting up a batch of B costs $80. Each unit of A generates a profit of $17 while a unit of B earns a profit of $21. The company can sell all the units it produces. The data for the problem are summarized below.
Operation A B Hours Cutting 3 4 48 Welding 2 1 36 The decision variables are defined as
Xi = the amount of product i produced
Yi = 1 if Xi > 0 and 0 if Xi = 0
What is the appropriate value for M1 in the linking constraint for product A?
(Multiple Choice)
4.7/5  (30)
(30)
A sub-problem in a B & B is solved and found infeasible. Should the B & B algorithm continue further analysis on this candidate problem?
(Multiple Choice)
4.9/5  (28)
(28)
An investor has $500,000 to invest and wants to maximize the money they will receive at the end of one year. They can invest in condos, apartments and houses. The profit after one year, the cost and the number of units available are shown below.
Formulate the ILP for this problem.
Profit Cost Number Variable Investment (\ 1,000) (\ 1,000) Available Condos 6 50 10 Apartments 12 90 5 Houses 9 100 7
(Essay)
4.8/5  (40)
(40)
An ILP problem has 5 binary decision variables. How many possible integer solutions are there to this problem?
(Multiple Choice)
4.9/5  (31)
(31)
Exhibit 6.1
The following questions pertain to the problem, formulation, and spreadsheet implementation below.
A research director must pick a subset of research projects to fund over the next five years. He has five candidate projects, not all of which cover the entire five-year period. Although the director has limited funds in each of the next five years, he can carry over unspent research funds into the next year. Additionally, up to $30K can be carried out of the five-year planning period. The following table summarizes the projects and budget available to the research director.
Project 1 2 3 4 5 (in \ 000 s) 1 \ 70 \ 40 \ 30 \ 15 \ 15 \ 160 2 \ 82 \ 35 \ 20 \ 20 \ 10 \ 190 3 \ 55 \ 10 \ 10 \ 5 \ 125 4 \ 69 \ 17 \ 15 \ 12 \ 8 \ 139 5 \ 75 \ 20 \ 25 \ 30 \ 45 \ 174 Budget \ 225 \ 60 \ 60 \ 50 \ 50
The following is the ILP formulation and a spreadsheet model for the problem.
if project 1 not selected, 1 if project 1 selected for ,
MAX 160+190+125+139+174 Subject to: 70+82+55+69+75+=225 40+35+10+17+20+=60+ 30+20+10+15+25+=60+ 15+20+5+12+30+=50+ 15+10+8+45+=50+ \leq30 binary ,\geq0
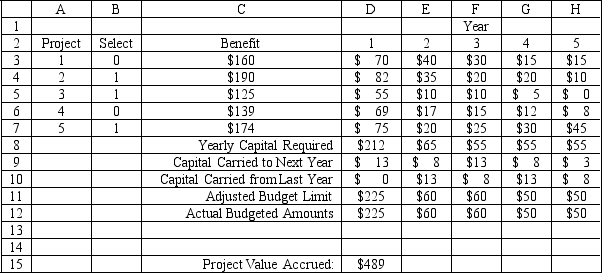 -Refer to Exhibit 6.1. What formulas should go in cells D8:H8 and D11:H11 of the above Excel spreadsheet?
-Refer to Exhibit 6.1. What formulas should go in cells D8:H8 and D11:H11 of the above Excel spreadsheet?
(Essay)
4.8/5  (32)
(32)
For maximization problems, the optimal objective function value to the LP relaxation provides what for the optimal objective function value of the ILP problem?
(Multiple Choice)
4.8/5  (37)
(37)
A company will be able to obtain a quantity discount on component parts for its three products, X1, X2 and X3 if it produces beyond certain limits. To get the X1 discount it must produce more than 50 X1's. It must produce more than 60 X2's for the X2 discount and 70 X3's for the X3 discount. How many binary variables are required in the formulation of this problem?
(Multiple Choice)
4.8/5  (34)
(34)
An integrality condition indicates that some (or all) of the
(Multiple Choice)
4.9/5  (28)
(28)
Consider the constraint X3 + X4 + X5 + X6 + X7 27
Representing Air Express' Monday minimum worker requirement. Why was a " " used versus an "="?
(Multiple Choice)
4.9/5  (29)
(29)
If a company produces Product 1, then it must produce at least 150 units of Product 1. Which of the following constraints enforces this condition?
(Multiple Choice)
4.8/5  (28)
(28)
One approach to solving integer programming problems is to ignore the integrality conditions and solve the problem with continuous decision variables. This is referred to as
(Multiple Choice)
4.9/5  (48)
(48)
Exhibit 6.1
The following questions pertain to the problem, formulation, and spreadsheet implementation below.
A research director must pick a subset of research projects to fund over the next five years. He has five candidate projects, not all of which cover the entire five-year period. Although the director has limited funds in each of the next five years, he can carry over unspent research funds into the next year. Additionally, up to $30K can be carried out of the five-year planning period. The following table summarizes the projects and budget available to the research director.
Project 1 2 3 4 5 (in \ 000 s) 1 \ 70 \ 40 \ 30 \ 15 \ 15 \ 160 2 \ 82 \ 35 \ 20 \ 20 \ 10 \ 190 3 \ 55 \ 10 \ 10 \ 5 \ 125 4 \ 69 \ 17 \ 15 \ 12 \ 8 \ 139 5 \ 75 \ 20 \ 25 \ 30 \ 45 \ 174 Budget \ 225 \ 60 \ 60 \ 50 \ 50
The following is the ILP formulation and a spreadsheet model for the problem.
if project 1 not selected, 1 if project 1 selected for ,
MAX 160+190+125+139+174 Subject to: 70+82+55+69+75+=225 40+35+10+17+20+=60+ 30+20+10+15+25+=60+ 15+20+5+12+30+=50+ 15+10+8+45+=50+ \leq30 binary ,\geq0
 -Refer to Exhibit 6.1. What values would you enter in the Risk Solver Platform (RSP) task pane for the above Excel spreadsheet?
Objective Cell:
Variables Cells:
Constraints Cells:
-Refer to Exhibit 6.1. What values would you enter in the Risk Solver Platform (RSP) task pane for the above Excel spreadsheet?
Objective Cell:
Variables Cells:
Constraints Cells:
(Essay)
4.9/5  (35)
(35)
Showing 21 - 40 of 72
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)