Exam 3: Exponential and Logarithmic Functions
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
Solve the exponential equation algebraically.Approximate the result to three decimal places.
(Multiple Choice)
4.9/5  (40)
(40)
$2500 is invested in an account at interest rate r, compounded continuously.Find the time required for the amount to double.(Approximate the result to two decimal places.)
(Multiple Choice)
4.8/5  (36)
(36)
Evaluate the logarithm using the change-of-base formula.Round your result to three decimal places.
Log15 1,500
(Multiple Choice)
5.0/5  (33)
(33)
Solve the logarithmic equation algebraically.Approximate the result to three decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Evaluate the logarithm log7 126 using the change of base formula.Round to 3 decimal places.
(Multiple Choice)
4.8/5  (31)
(31)
The chemical acidity of a solution is measured in units of pH: , where is the hydrogen ion concentration in the solution.If a sample of rain has a pH of 3.3, how many times higher is its than pure water's, which has a pH of 7?
(Multiple Choice)
4.8/5  (42)
(42)
The population P (in thousands) of Orlando, Florida from 2000 through 2007 can be modeled by where t represents the year, with corresponding to 2000.In 2006, the population of Orlando, Florida was about 1,883,000.00.Find the value of k.
(Multiple Choice)
4.8/5  (32)
(32)
Find the value of b that would cause the graph of y = bx to look like the graph below. 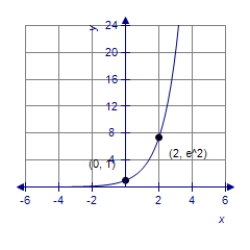
(Multiple Choice)
4.7/5  (36)
(36)
The populations P (in thousands) of Pittsburgh, Pennsylvania from 2000 through 2007 can be modeled by where t represents the year, with corresponding to 2000.Use the model to find the numbers of cell sites in the year 2009.
(Multiple Choice)
4.9/5  (30)
(30)
Rewrite the logarithm as a ratio of natural logarithms.
Log1/5 x
(Multiple Choice)
4.7/5  (28)
(28)
Evaluate the function at the indicated value of .Round your result to three decimal places.
(Multiple Choice)
4.9/5  (31)
(31)
Use a graphing utility to construct a table of values for the function.Round your answer to three decimal places.
(Multiple Choice)
4.8/5  (39)
(39)
Use a graphing utility to construct a table of values for the function.Round your answer to three decimal places.
(Multiple Choice)
4.9/5  (29)
(29)
Assume that x, y, and z are positive numbers.Use the properties of logarithms to write the expression as the logarithm of one quantity.
(Multiple Choice)
4.9/5  (45)
(45)
Showing 81 - 100 of 266
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)