Exam 3: Exponential and Logarithmic Functions
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
Solve the exponential equation algebraically.Approximate the result to three decimal places.
(Multiple Choice)
4.8/5  (31)
(31)
Find the exact value of the logarithmic expression without using a calculator.
5 ln e7
(Multiple Choice)
4.8/5  (39)
(39)
Determine whether the statement is true or false given that f(x) = ln x.
f(x - 7) = f(x) - f(7), x > 0
(True/False)
4.8/5  (29)
(29)
Find the exponential model that fits the points shown in the graph. 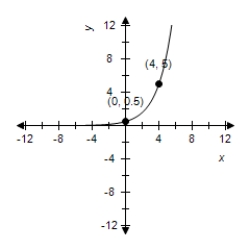
(Multiple Choice)
4.7/5  (34)
(34)
Use a calculator to find the value for to four decimal places.
(Multiple Choice)
4.8/5  (23)
(23)
Solve the exponential equation algebraically.Approximate the result to three decimal places.
(Multiple Choice)
4.8/5  (25)
(25)
The population P of a culture of bacteria is described by the equation , where t is the time, in hours, relative to the time at which the population was 1600.
(a) What was the population at hours? Show your work.
(b) After how many hours will the population reach 10000.00? Round to the nearest tenth of an hour.Show your work.
(Essay)
4.7/5  (29)
(29)
Evaluate the function at the indicated value of .Round your result to three decimal places.
(Multiple Choice)
4.9/5  (40)
(40)
Solve the exponential equation algebraically.Approximate the result to three decimal places.
(Multiple Choice)
4.8/5  (35)
(35)
Find the exponential model that fits the points shown in the graph. 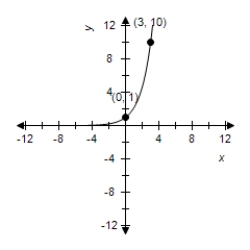
(Multiple Choice)
4.8/5  (43)
(43)
The population P of a culture of bacteria is described by the equation , where t is the time, in hours, relative to the time at which the population was 1300.What was the population at hours?
(Multiple Choice)
4.8/5  (42)
(42)
Condense the expression to the logarithm of a single quantity.
(Multiple Choice)
4.8/5  (39)
(39)
Showing 161 - 180 of 266
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)