Exam 8: Matrices and Determinants
Exam 1: Functions and Their Graphs513 Questions
Exam 2: Polynomial and Rational Functions456 Questions
Exam 3: Exponential and Logarithmic Functions266 Questions
Exam 4: Trigonometry384 Questions
Exam 5: Analytic Trigonometry265 Questions
Exam 6: Additional Topics In Trigonometery304 Questions
Exam 7: Systems Of Equations and Inequalities305 Questions
Exam 8: Matrices and Determinants283 Questions
Exam 9: Sequences Series and Probability405 Questions
Exam 10: Topics In Analytic Geometry556 Questions
Exam 11: Analytic Geometry In Three Dimensions256 Questions
Exam 12: Limits and An Introduction To Calculus259 Questions
Select questions type
Find a value of y such that the triangle with the given vertices has an area of 8 square units.
(5, 6), (5, 8), (-3, y)
(Multiple Choice)
4.8/5  (43)
(43)
Use matrices to solve the system of equations (if possible).Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.
(Multiple Choice)
4.9/5  (36)
(36)
Solve the system of linear equations using an inverse matrix.
(Multiple Choice)
4.9/5  (35)
(35)
Use the inverse formula to find the inverse of the 2×2 matrix (if it exists).
(Multiple Choice)
4.8/5  (31)
(31)
Use a determinant and the given vertices of a triangle to find the area of the triangle. 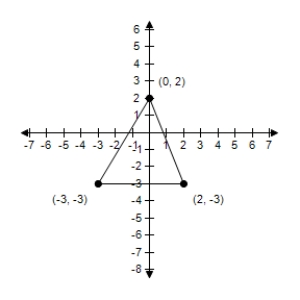
(Multiple Choice)
4.9/5  (24)
(24)
Write the system of linear equations as a matrix equation AX = B, and use Gauss-Jordan elimination on the augmented matrix to solve for the matrix X.
(Multiple Choice)
4.9/5  (35)
(35)
Find the uncoded 1 × 3 row matrices for the message "TWO IF BY LAND"; then encode the message using the encoding matrix .Show all your work.
(Essay)
4.7/5  (35)
(35)
Evaluate the determinant in which the entries are functions.
(Multiple Choice)
4.8/5  (33)
(33)
Use matrices to solve the system of equations (if possible).Use Gaussian elimination with back-substitution or Gauss-Jordan elimination.
(Multiple Choice)
4.8/5  (41)
(41)
Use a determinant to find an equation of the line passing through the points.
(0, 0), (3, 5)
(Multiple Choice)
4.9/5  (31)
(31)
Write the system of linear equations as a matrix equation, AX = B.
(Multiple Choice)
4.8/5  (39)
(39)
The currents in an electrical network are given by the solution of the system
Where I1, I2 and I3 are measured in amperes.Solve the system of equations using matrices.
(Multiple Choice)
4.9/5  (25)
(25)
The currents in an electrical network are given by the solutions of the system where I1, I2, and I3 are measured in amperes.Solve the system of equations using matrices.
(Multiple Choice)
4.9/5  (22)
(22)
Showing 121 - 140 of 283
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)