Exam 8: Introduction to Probability

A bag contains 9 red balls and 15 white balls. Two balls are drawn without replacement. What is the probability that the second ball is red R, given that the first ball is white W? ​

In one state there is a lottery game called Pick 4. The state chooses 12 numbers from 46 numbers, and each player chooses 4 numbers from the same 46 numbers. If all 4 of a player's numbers are among the 12 numbers that the state picked, then that player is a "big winner." Find the probability of being a big winner. Round your answer to four decimal places. ​

The following table gives the numbers of AIDS deaths in a single year for people over age 13 in various categories. Use the table to find the probability, rounded to four decimal places, that a person who died of AIDS in this year was female. ​ ​

Assuming there are 365 different birthdays, find the probability that at least two of nine people chosen at random will have same birthdays. Round your answer to five decimal places. ​

From a deck of 52 playing cards, two cards are drawn, one after the other without replacement. What is the probability that the first will be an ace nd the second will be an ace? ​

A dry cleaning firm has 6 employees: 4 women and 2 men. 2 of the women and 1 of the men are 42 years old or older. The remainder are over 20 years of age and under 42. If a person is chosen at random from this firm, what is the probability that the person is under 42 years of age? ​

Suppose that an employer plans to hire six people from a group of nine equally qualified people, of whom two are minority candidates. If the employer does not know which candidates are minority candidates, and if she selects her employees at random, what is the probability that all two minority candidates are hired? Round your answer to six decimal places. ​

If 5% of all light bulbs a company manufactures are defective, the probability of any one bulb being defective is 0.05. What is the probability that four bulbs drawn independently from the company's stock will be defective? Round your answer to eight decimal places. ​

A bag contains 5 white balls and 5 red balls. Construct a probability tree to determine the probability that if 2 balls are drawn, with replacement, the first ball is red R or the second is white W. ​

The following table gives the numbers of AIDS deaths in a single year for people over age 13 in various categories. Use the table to find the probability, rounded to four decimal places, that a person who died of AIDS in this year was female or Hispanic. ​ ​

The probability that daughters of a mother who attends church regularly will also attend church regularly is 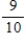, whereas the probability that daughters of a mother who does not attend regularly will attend regularly is 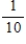. What is the steady-state vector for this information? ​

A ball is drawn from a bag containing 9 red balls numbered 1-9 and 7 white balls numbered 10-16. What is the probability that the ball is white W or odd-numbered O? ​

What is the probability of being dealt a poker hand of 5 cards containing exactly 5 cards of the same suit? Round your answer to six decimal places. ​

A box of 26 transistors has 3 defective ones. If 2 transistors are drawn from the box together, what is the probability that neither transistor is defective? Round your answer to four decimal places. ​

A survey questioned 1000 people regarding raising the legal drinking age from 18 to 21. Of the 560 people who favored raising the legal drinking age, 390 were female. Of the 440 opposition responses, 120 were female. If a person selected at random from this group is a man, what is the probability that the person favors raising the drinking age? ​

A ball is drawn from a bag containing 3 red balls numbered 1-3 and 13 white balls numbered 4-16. What is the probability that the number on the ball is odd O? ​

An urn contains five red balls numbered 1, 2, 3, 4 and 5, four white balls numbered 6, 7, 8 and 9, and three black balls numbered 10, 11 and 12. A ball is drawn from the urn. What is the probability that it is an odd-numbered ball O? ​

Each computer component that the Peggos Company produces is tested twice before it is shipped. There is a 0.7 probability that a defective component will be so identified by the first test and a 0.8 probability that it will be identified as being defective by the second test. What is the probability that a defective component will not be identified as defective before it is shipped? ​

Five percent of the population of the United States has type AB blood. What is the probability, rounded to two decimal places, that a U.S. resident chosen at random will have type AB blood? ​

A man owns an Audi, a Ford, and a VW. He drives everyday and never drives the same car two days in a row. These are the probabilities that he drives each of the other cars the next day: ​ Pr(Ford after Audi) = 0.5 Pr(VW after Audi) = 0.5 Pr(Audi after Ford) = 0.6 Pr(VW after Ford) = 0.4 Pr(Audi after VW) = 0.9 Pr(Ford after VW) = 0.1 ​ If he drove the Ford on Monday, what is the probability that he will drive the VW on Wednesday? ​