Exam 8: Introduction to Probability
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
The following table gives the percent of employees of the Ace Company in each of three salary brackets, categorized by the sex of the employees. An employee is selected at random. What is the probability that the person selected is female and makes less than $30,000? 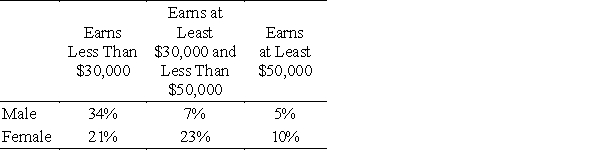
(Multiple Choice)
4.9/5  (34)
(34)
The probability that a wife W watches a certain television show is 0.31, that her husband H watches it is 0.21, and that both watch the show is 0.05. What is the probability, to two decimal places, that either the husband or the wife watches this show?
(Multiple Choice)
4.7/5  (34)
(34)
A man owns an Audi, a Ford, and a VW. He drives every day and never drives the same car two days in a row. These are the probabilities that he drives each of the other cars the next day:
Pr(Ford after Audi) = 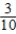 Pr(VW after Audi) =
Pr(VW after Audi) = 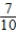 Pr(Audi after Ford) =
Pr(Audi after Ford) = 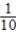 Pr(VW after Ford) =
Pr(VW after Ford) = 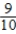 Pr(Audi after VW) =
Pr(Audi after VW) =  Pr(Ford after VW) =
Pr(Ford after VW) = 
What is the steady-state vector for this problem?
What is the steady-state vector for this problem?
(Multiple Choice)
4.8/5  (34)
(34)
A bag contains 4 red balls and 11 white balls. Two balls are drawn from the bag. What is the probability that the second ball is white W, given that the first ball is red and is replaced before the second is drawn?
(Multiple Choice)
4.7/5  (32)
(32)
The probability that daughters of a mother who attends church regularly will also attend church regularly is 0.9, whereas the probability that daughters of a mother who does not attend regularly will attend regularly is 0.2.
If a woman attends church regularly and has one daughter, who in turn has one daughter, what is the probability that the granddaughter attends church regularly? Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (35)
(35)
The 2003 Toyota Matrix was first made available with 5 different engines and with 6 levels of trim, plus either front-wheel or all-wheel drive. How many different Toyota Matrix cars models were available for purchase?
(Multiple Choice)
4.8/5  (32)
(32)
Suppose a country has 1,000,000 registered voters, 370,000 of whom are Democrats and 430,000 of whom are Republicans. If a registered voter is chosen at random, what is the probability that he or she is neither a Democrat nor a Republican?
(Multiple Choice)
4.8/5  (36)
(36)
For species that reproduce sexually, characteristics are determined by a gene from each parent. Suppose that for a certain trait there are two possible genes available from each parent: a dominant gene D and a recessive gene r. Then the different gene combinations (called genotypes) for the offspring are DD, Dr, rD, and rr, where Dr and rD produce the same trait. Suppose further that these genotypes are the states of a Markov chain with the transition matrix given below. If the initial occurrence of those genotypes in the population is 0.1 for DD, 0.2 for Dr, and 0.7 for rr, find the distribution (probability) of each type of the second generation of offspring. Round all numerical values in your answer to two decimal places. 
(Multiple Choice)
4.8/5  (33)
(33)
If the first digit of a seven-digit telephone number cannot be a 0 or 1, what is the probability that a number chosen at random will have all seven digits the same?
(Multiple Choice)
4.7/5  (37)
(37)
The following table gives the results of a 2005 survey of 1000 people regarding the funding of universal health care by employers (employer mandate).  What is the probability that a person selected at random from this group will favor universal health care F with an employer mandate, given that the person is a Democrat D?
What is the probability that a person selected at random from this group will favor universal health care F with an employer mandate, given that the person is a Democrat D?
(Multiple Choice)
4.9/5  (34)
(34)
If the probability that an event will occur is 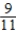 , what are the odds in favor of the event occurring?
, what are the odds in favor of the event occurring?
(Multiple Choice)
4.9/5  (41)
(41)
A local business A has two competitors, B and C. No customer patronizes more than one of these businesses at the same time. Initially, the probabilities that a customer patronizes A, B, or C are 0.2, 0.6, and 0.2, respectively. Suppose A initiates an advertising campaign to improve its business and finds the following transition matrix to describe the effect. 
Find the steady-state vector for this market-that is, the long-range share of the market that each business can expect if the transition matrix holds.
Find the steady-state vector for this market-that is, the long-range share of the market that each business can expect if the transition matrix holds.
(Multiple Choice)
4.8/5  (28)
(28)
Use the transition matrix  and initial probability vector
and initial probability vector 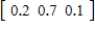 to find the resulting third probability vector. Round all numerical values in your answer to three decimal places.
to find the resulting third probability vector. Round all numerical values in your answer to three decimal places.
(Multiple Choice)
4.7/5  (32)
(32)
In a certain city, the Democratic, Republican, and Consumer parties have members of their parties on the city council. The probability of a member of this party winning in any election depends on the proportional membership of his/her party at the time of the election. The probabilities for all these parties winning are given by the following transition matrix P. Using the given transition matrix and assuming the initial-probability vector is 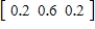 , find the probability vectors for the next four steps of the Markov chain. Round all numerical values in your answer to four decimal places.
, find the probability vectors for the next four steps of the Markov chain. Round all numerical values in your answer to four decimal places. 
(Multiple Choice)
4.9/5  (37)
(37)
One ball is drawn at random from a bag containing 6 red R balls and 10 white W balls. What is the probability that the ball is red or white?
(Multiple Choice)
4.8/5  (27)
(27)
An urn contains two red R balls numbered 1 and 2, five white W balls numbered 3, 4, 5, 6 and 7, and three black B balls numbered 8, 9 and 10. A ball is drawn from the urn. What is the probability that it is red or odd-numbered O?
(Multiple Choice)
4.9/5  (32)
(32)
An ordinary die is tossed. What is the probability of getting an even number or a number divisible by 6?
(Multiple Choice)
4.9/5  (32)
(32)
How many four-digit numbers can be formed from the digits 1, 3, 5, 7, 8, and 9 if the numbers mast be even and digits are not repeated? (Hint: Begin with the digit where there is a restriction on the choices.)
(Multiple Choice)
4.8/5  (28)
(28)
Showing 121 - 140 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)