Exam 15: Functions of Two or More Variables
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
Suppose that x units of one input and y units of a second input result in 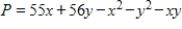 units of a product. What is the maximum production?
units of a product. What is the maximum production?
(Multiple Choice)
4.9/5  (38)
(38)
Suppose that the production function for a product is 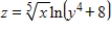 , where x represents the number of work hours and y represents the available capital (per week). Find the marginal productivity of y.
, where x represents the number of work hours and y represents the available capital (per week). Find the marginal productivity of y.
(Multiple Choice)
4.8/5  (25)
(25)
The cost per day to society of an epidemic is 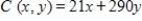 , where C is in dollars, x is the number of people infected on a given day, and y is the number of people who die on a given day. If 18,500 people are infected and 10 people die on a given day, what is the cost to society? Round your answer to the nearest dollar.
, where C is in dollars, x is the number of people infected on a given day, and y is the number of people who die on a given day. If 18,500 people are infected and 10 people die on a given day, what is the cost to society? Round your answer to the nearest dollar.
(Multiple Choice)
4.9/5  (36)
(36)
A firm has two plants, X and Y. Suppose that the cost of producing x units at plant X is 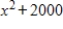 dollars and the cost of producing y units of the same product at plant Y is given by
dollars and the cost of producing y units of the same product at plant Y is given by 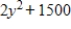 dollars. If the firm has an order for 3,000 units, how many should it produce at each plant to fill this order and minimize the cost of production?
dollars. If the firm has an order for 3,000 units, how many should it produce at each plant to fill this order and minimize the cost of production?
(Multiple Choice)
4.8/5  (32)
(32)
Find the maximum value of 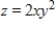 subject to
subject to 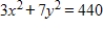 ,
, 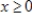 ,
, 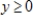 . Round your answer to the nearest integer.
. Round your answer to the nearest integer.
(Multiple Choice)
4.8/5  (31)
(31)
Suppose that the number of crates of an agricultural product is given by 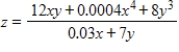 , where x is the number of hours of and y is the number of acres of the crop. Find the marginal productivity of the number of hours of labor when
, where x is the number of hours of and y is the number of acres of the crop. Find the marginal productivity of the number of hours of labor when 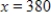 and
and 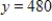 .
.
(Multiple Choice)
4.8/5  (30)
(30)
Find the slope of the tangent in the positive x-direction to the surface 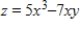 at the point
at the point 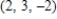 .
.
(Multiple Choice)
4.9/5  (37)
(37)
The joint cost (in dollars) for two products is given by 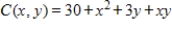 , where x represents the quantity of product X produced and y represents the quantity of product Y produced. Find the marginal cost with respect to x if 2 units of product X and 9 units of product Y are produced.
, where x represents the quantity of product X produced and y represents the quantity of product Y produced. Find the marginal cost with respect to x if 2 units of product X and 9 units of product Y are produced.
(Multiple Choice)
4.9/5  (37)
(37)
There are different models for measuring the effects of high temperature and humidity. One of these is the Summer Simmer Index (S), given by 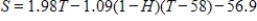 , where T is the air temperature (in degrees Fahrenheit) and H is the relative humidity (expressed as a decimal).
In a certain city, the measured temperature and humidity on a given day are:
Maximum:
, where T is the air temperature (in degrees Fahrenheit) and H is the relative humidity (expressed as a decimal).
In a certain city, the measured temperature and humidity on a given day are:
Maximum: 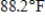 with 47% humidity
Minimum:
with 47% humidity
Minimum: 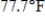 with 78% humidity
Calculate the Summer Simmer Index S for both the maximum and minimum temperatures.
with 78% humidity
Calculate the Summer Simmer Index S for both the maximum and minimum temperatures.
(Multiple Choice)
4.9/5  (31)
(31)
Suppose that the production function for a product is 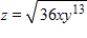 , where x represents the number of work hours per month and y is the number of available machines. Determine the marginal productivity of x.
, where x represents the number of work hours per month and y is the number of available machines. Determine the marginal productivity of x.
(Multiple Choice)
4.9/5  (32)
(32)
Suppose that 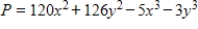 tons is the production function for a product with x units of one input and y units of a second input. Find the values of x and y that will maximize production.
tons is the production function for a product with x units of one input and y units of a second input. Find the values of x and y that will maximize production.
(Multiple Choice)
4.8/5  (42)
(42)
Find x and y such that 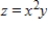 subject to
subject to 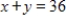 ,
, 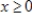 ,
, 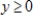 attains a maximum value.
attains a maximum value.
(Multiple Choice)
4.9/5  (40)
(40)
Find the slope of the tangent in the positive  -direction to the surface
-direction to the surface 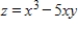 at
at 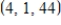 .
.
(Multiple Choice)
4.9/5  (26)
(26)
Showing 21 - 40 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)