Exam 15: Functions of Two or More Variables
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
Find the dimensions (in centimeters) of the box with square base, open top, and volume 1,098,500 cubic centimeters that requires the least materials to make.
(Multiple Choice)
4.8/5  (39)
(39)
Suppose that the utility function for two commodities is given by 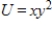 and that the budget constraint is
and that the budget constraint is 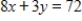 . What values of x and y will maximize utility?
. What values of x and y will maximize utility?
(Multiple Choice)
4.7/5  (46)
(46)
Find the maximum value of the function 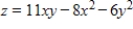 subject to the condition
subject to the condition 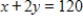 .
.
(Multiple Choice)
4.9/5  (40)
(40)
A company has the Cobb-Douglas production function 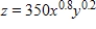 , where x is the number of units of labor, y is the number of units of capital, and z is the units of production. Suppose labor costs $200 per unit, capital costs $150 per unit, and the total cost of labor and capital is limited to $300,000. Find the number of units of labor and the number of units of capital that maximize production.
, where x is the number of units of labor, y is the number of units of capital, and z is the units of production. Suppose labor costs $200 per unit, capital costs $150 per unit, and the total cost of labor and capital is limited to $300,000. Find the number of units of labor and the number of units of capital that maximize production.
(Multiple Choice)
4.8/5  (35)
(35)
Suppose that the joint cost function in dollars for two products is 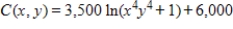 . Find the marginal cost with respect to y.
. Find the marginal cost with respect to y.
(Multiple Choice)
4.8/5  (31)
(31)
Suppose that the following table shows the average hourly earnings for full-time production workers in various industries for selected years. The linear regression equation for hourly earnings as a function of time is given by 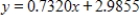 (where x is the number of years after 1970 and y is the average hourly wage). What does this model predict for the average hourly earnings in 2024? Round your answer to two decimal places.
(where x is the number of years after 1970 and y is the average hourly wage). What does this model predict for the average hourly earnings in 2024? Round your answer to two decimal places. 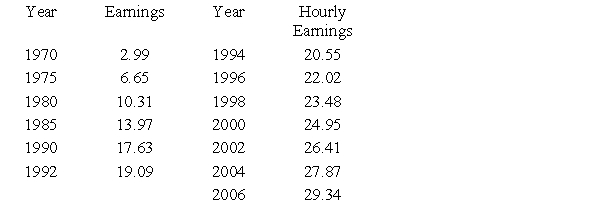
(Multiple Choice)
4.9/5  (27)
(27)
Suppose wind and cold temperatures combine to make the air temperature feel colder than it actually is. This combination is reported as wind chill. The following table shows that wind chill temperatures, WC, are a function of wind speed,  , and air temperature,
, and air temperature,  . If
. If 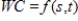 , use the table to find
, use the table to find 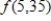 and interpret the answer.
Air Temperature
and interpret the answer.
Air Temperature 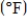

(Multiple Choice)
4.8/5  (23)
(23)
Find the values for each of the dimensions of a closed-top box of length x, width y, and height z (in inches) if the volume equals 32,768 cubic inches and the box requires the least amount of material to make.
(Multiple Choice)
4.9/5  (31)
(31)
In economics, the most economical quantity Q of goods (TVs, dress, gallons of paint, etc.) for a store to order is given by Wilson's lot size formula 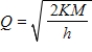 , where K is the cost of placing the order, M is the number of items sold per week, and h is the weekly holding costs for each item (the cost of storage space, utilities, taxes, security, etc.). Calculate
, where K is the cost of placing the order, M is the number of items sold per week, and h is the weekly holding costs for each item (the cost of storage space, utilities, taxes, security, etc.). Calculate 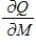 for
for 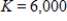 ,
, 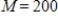 , and
, and 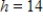 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (30)
(30)
Suppose that a manufacturer produces two brands of a product, brand 1 and brand 2. Suppose the demand for brand 1 is 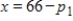 thousand units and the demand for brand 2 is
thousand units and the demand for brand 2 is 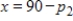 thousand units, where p1 and p2 prices in dollars. If the joint cost function is
thousand units, where p1 and p2 prices in dollars. If the joint cost function is 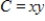 , in thousands of dollars, how many of each brand should be produced to maximize profit?
, in thousands of dollars, how many of each brand should be produced to maximize profit?
(Multiple Choice)
4.8/5  (39)
(39)
Suppose that a gas satisfies the universal gas law, 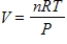 with n equal to 40 moles of the gas and R, the universal gas constant, equal to 0.082054. What is V if
with n equal to 40 moles of the gas and R, the universal gas constant, equal to 0.082054. What is V if 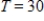 (kelvins, the units in which temperature is measured on the Kelvin scale) and
(kelvins, the units in which temperature is measured on the Kelvin scale) and 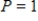 atmosphere? Round your answer to four decimal places.
atmosphere? Round your answer to four decimal places.
(Multiple Choice)
4.9/5  (41)
(41)
Showing 101 - 119 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)