Exam 1: Overview and Descriptive Statistics
The number of contaminating particles on a silicon wafer prior to a certain rinsing process was determined for each wafer in a sample size 100, resulting in the following frequencies: Number of particles Frequency Number of particles Frequency 0 1 8 12 1 2 9 4 2 3 10 5 3 12 11 3 4 11 12 1 5 15 13 2 6 18 14 1 7 10
a. What proportion of the sampled wafers had at least two particles? At least six particles?
b. What proportion of the sampled wafers had between four and nine particles, inclusive? Strictly between four and nine particles?
a. From this frequency distribution, the proportion of wafers that contained at least two particles is (100-1-2)/100 = .97, or 97%. In a similar fashion, the proportion containing at least 6 particles is (100 - 1-2-3-12-11-15)/100 = 56/100 = .56, or 56%.
b. The proportion containing between 4 and 9 particles inclusive is (11+15+18+10+12+4)/100 = 70/100 = .70, or 70%. The proportion that contain strictly between 4 and 9 (meaning strictly more than 4 and strictly less than 9) is (15+ 18+10+12)/100= 55/100 = .55, or 55%.
Temperature transducers of a certain type are shipped in batches of 50. A sample of 60 batches was selected, and the number of transducers in each batch not conforming to design specifications was determined, resulting in the following data: 0 4 2 1 3 1 1 3 4 1 2 3 2 2 8 4 5 1 3 1 2 1 2 4 0 1 3 2 0 5 3 3 1 3 2 4 7 0 2 3 5 0 2 3 2 1 0 6 4 2 1 6 0 3 3 3 6 1 2 3
a. Determine frequencies and relative frequencies for the observed values of x = number of nonconforming transducers in a batch.
b. What proportion of batches in the sample has at most four nonconforming transducers? What proportion has fewer than four? What proportion has at least four nonconforming units?
a. 1.001
The relative frequencies don't add up exactly to 1because they have been rounded
b. The number of batches with at most 4 nonconforming items is 7+12+13+14+6=52, which is a proportion of 52/60=.867. The proportion of batches with (strictly) fewer than 4 nonconforming items is 46/60=.767.
Answer the following two questions:
a. If a constant c is added to each
in a sample, yielding
=
+ c, how do the sample mean and median of the
's relate to the mean and median of the
's? Verify your conjectures.
b. If each
is multiplied by a constant c, yielding
=
, answer the question of part (a). Again, verify your conjectures.
a. = the median of = median of b. =
Consider the following observations on shear strength of a joint bonded in a particular manner: 30.0 4.4 33.1 66.7 81.5 22.2 40.4 16.4 73.7 36.6 109.9
a. Determine the value of the sample mean.
b. Determine the value of the sample median. Why is it so different from the mean?
c. Calculate a trimmed mean by deleting the smallest and largest observations. What is the corresponding trimming percentage? How does the value of this 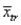 compare to the mean and median?
compare to the mean and median?
The cumulative frequency and cumulative relative frequency for a particular class interval are the sum of frequencies and relative frequencies, respectively, for that interval and all intervals lying below it. Compute the cumulative frequencies and cumulative relative frequencies for the following data: 75 89 80 93 64 67 72 70 66 85 89 81 81 71 74 82 85 63 72 81 81 95 84 81 80 70 69 66 60 83 85 98 84 68 90 82 69 72 87 88
A sample of 26 offshore oil workers took part in a simulated escape exercise, resulting in the accompanying data on time (sec) to complete the escape: 373 370 364 366 364 325 339 393 356 359 363 375 424 325 394 402 392 369 374 359 356 403 334 397
a. Construct a stem-and-leaf display of the data. How does it suggest that the sample mean and median will compare?
b. Calculate the values of the sample mean and median.
c. By how much could the largest time, currently 424, be increased without affecting the value of the sample median? By how much could this value be decreased without affecting the value of the sample mean?
d. What are the values of
and
when the observations are re-expressed in minutes?
A Southern State University system consists of 23 campuses. An administrator wishes to make an inference about the average distance between the hometowns of students and their campuses. Describe and discuss several different sampling methods that might be employed. Would this be an enumerative or an analytic study? Explain your reasoning.
Calculate and interpret the values of the sample mean and sample standard deviation for the following observations on fracture strength. 128 131 142 168 87 93 105 114 96
A sample of n = 10 automobiles was selected, and each was subjected to a 5-mph crash test. Denoting a car with no visible damage by S (for success) and a car with such damage by F, results were as follows: S S S F F S S F S S
a. What is the value of the sample proportion of successes x/n?
b. Replace each S with a 1 and each F with a 0. Then calculate
for this numerically coded sample. How does
compare to x/n?
c. Suppose it is decided to include 15 more cars in the experiment. How many of these would have to be S's to x/n = .80 for the entire sample of 25 cars?
A sample of 20 glass bottles of a particular type was selected, and the internal pressure strength of each bottle was determined. Consider the following partial sample information:
Median = 202.2
lower fourth = 196.0
Upper fourth = 216.8 Three smallest observations 125.8 188.1 193.7 Three largest observations 221.3 230.5 250.2 Are there any outliers in the sample? Any extreme outliers?
The first four deviations from the mean in a sample of n = 5 reaction times were .6, .9, 1.0, and 1.5. What is the fifth deviation from the mean? Give a sample for which these are the five deviations from the mean.
The accompanying data specific gravity values for various wood types used in construction . .41 .41 .42 .42. .42 .42 .42 .43 .44 .54 .55 .58 .62 .66 .66 .67 .68 .75 .31 .35 .36 .36 .37 .38 .40 .40 .40 .45 .46 .46 .47 .48 .48 .48 .51 .54 Construct a stem-and-leaf display using repeated stems and comment on any interesting features of the display.
An experiment was carried out to study how flow rate through a solenoid valve in an automobile's pollution-control system depended on three factors: armature lengths, spring load, and bobbin depth. Two different levels (low and high) of each factor were chosen, and a single observation on flow was made for each combination of levels.
a. The resulting data set consisted of how many observations?
b. Is this an enumerative or analytic study? Explain your reasoning.
A Michigan city divides naturally into ten district neighborhoods. How might a real estate appraiser select a sample of single-family homes that could be used as a basis for developing an equation to predict appraised value from characteristics such as age, size, number of bathrooms, and distance to the nearest school, and so on? Is the study enumerative or analytic?
Give one possible sample of size 4 from each of the following populations:
a. All daily newspapers published in the United States
b. All companies listed on the New York Stock Exchange
c. All students at your college or university
d. All grade point averages of students at your college or university
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)