Exam 11: Multifactor Analysis of Variance
Exam 1: Overview and Descriptive Statistics15 Questions
Exam 2: Probability16 Questions
Exam 3: Discrete Random Variables and Probability Distributions22 Questions
Exam 4: Continuous Random Variables and Probability Distributions17 Questions
Exam 5: Joint Probability Distributions and Random Samples19 Questions
Exam 6: Point Estimation28 Questions
Exam 7: Statistical Intervals Based on a Single Sample59 Questions
Exam 8: Tests of Hypotheses Based on a Single Sample92 Questions
Exam 9: Inferences Based on Two Samples73 Questions
Exam 10: The Analysis of Variance43 Questions
Exam 11: Multifactor Analysis of Variance62 Questions
Exam 12: Simple Linear Regression and Correlation106 Questions
Exam 13: Nonlinear and Multiple Regression77 Questions
Exam 14: Goodness-Of-Fit Tests and Categorical Data Analysis40 Questions
Exam 15: Distribution-Free Procedures66 Questions
Exam 16: Quality Control Methods86 Questions
Select questions type
A four-factor ANOVA experiment was carried out to investigate the effects of fabric (A), type of exposure (B), level of exposure (C), and fabric direction (D) on extent of color change in exposed fabric as measured by a spectrocolorimeter. Two observations were made for each of the three fabrics, two types, three levels, and two directions, resulting in MSA = 2207.329, MSB = 47.255, MSC = 491.783, MSD = .044, MSAB = 15.303, MSAC = 275.446, MSAD = .470, MSBC = 2.141, MSBD = .280, MSE = .977, and MST = 93.621 ("Accelerated Weathering of Marine Fabrics," J. Testing and Eval.,. 1992: 139-143). Assuming fixed effects for all factors, carry out an analysis of variance using for all tests and summarize your conclusions.
Free
(Essay)
4.8/5  (37)
(37)
Correct Answer:
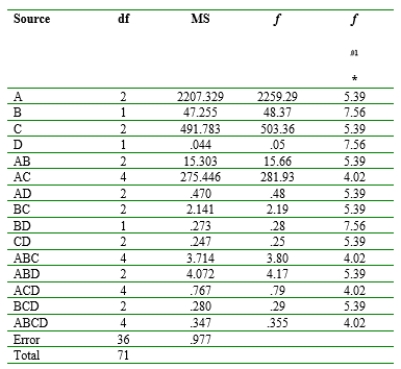 *Because denominator d.f. for 36 is not tabled, use d.f. = 30
*Because denominator d.f. for 36 is not tabled, use d.f. = 30
SST = (71) (93.621) = 6,647.091. Computing all other sums of squares and adding them up = 6,645.702. Thus SSABCD = 6,647.091 - 6,645.702 = 1,389 and At level .01 the statistically significant main effects are A, B, C. The interaction AB and AC are also statistically significant. No other interactions are statistically significant.
In the randomized block design for ANOVA where the single factor of primary interest has I levels, and b blocks are created to control for extraneous variability in experimental units or subjects, the number of degrees of freedom for SSE (error sum of squares) is given by
Free
(Multiple Choice)
4.8/5  (48)
(48)
Correct Answer:
B
The following equation SST = SSA + SSB +SSAB +SSE applies to which ANOVA model?
Free
(Multiple Choice)
4.7/5  (39)
(39)
Correct Answer:
B
The strength of concrete used in commercial construction tends to vary from one batch to another. Consequently, small test cylinders of concrete sampled from a batch are "cured" for periods up to about 28 days in temperature- and moisture-controlled environments before strength measurements are made. Concrete is then "bought and sold on the basis of strength test cylinders". The accompanying data resulted from an experiment carried out to compare three different curing methods with respect to compressive strength (MPa). Analyze this data. Batch Method A Method B Method C 1 30.2 33.2 30.0 2 28.6 30.1 32.1 3 29.5 31.7 30.0 4 31.4 34.1 33.0 5 30.0 32.5 31.9 6 26.4 28.8 27.3 7 27.7 27.9 30.2 8 31.9 31.9 33.1 9 26.1 29.0 28.7 10 28.1 28.9 32.7
(Essay)
4.9/5  (38)
(38)
In the fixed effects model with interaction, assume that there are I levels of factor A, J levels of Factor J, and K observations (replications) for each of the IJ combinations of levels of the two factors. Then SSE (the error sum of squares) has df = __________.
(Short Answer)
4.9/5  (42)
(42)
The number of miles useful tread wear (in 1000's) was determined for tires of five different makes of subcompact car (factor A, with I = 5) in combination with each of four different brands of radial tires (factor B, with J = 4), resulting in IJ = 20 observations. The values SSA = 30, SSB = 45, and SSE = 60 were then computed. Assume that an additive model is appropriate.
a. Test
(no differences in true average tire lifetime due to makes of cars) versus
using a level .05 test.
b.
(no differences in "true" average tire lifetime due to brands of tires) versus
using a level .05 test.
(Essay)
4.8/5  (45)
(45)
In a two-factor experiment where factor A consists of 5 levels, factor B consists of 4 levels, and there is only one observation on each of the 20 treatments, the critical value for testing the null hypothesis that the different levels of factor B have no effect on true average response at significance level .05 is denoted by __________, and is equal to __________.
(Essay)
4.8/5  (36)
(36)
In a three-factor experiment, if the levels of factor A are identified with the rows of a two-way table and the levels of B with the columns of the table, then the defining characteristic of a Latin square design is that every level of factor C appears exactly __________ in each row and exactly __________ in each column.
(Short Answer)
4.7/5  (30)
(30)
Which of the following statements are true regarding a two-factor experiment?
(Multiple Choice)
4.8/5  (36)
(36)
In the fixed effects model with interaction, assume that there are I levels of factor A, J levels of factor B, and K observations (replications) for each of the IJ combinations of levels of the two factors. Then SSAB (the interaction sum of squares) has df =__________.
(Short Answer)
4.8/5  (37)
(37)
Consider a experiment with 2 blocks. The price paid for this blocking is that __________ of the factor effects cannot be estimated.
(Short Answer)
4.8/5  (43)
(43)
The three-factor fixed effects model, with the same number of observations for each combination of levels I, J, and K of the three factors A, B, and C, respectively, is represented by 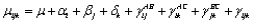 . Which of the following statements are true?
. Which of the following statements are true?
(Multiple Choice)
4.8/5  (36)
(36)
The following summary quantities were computed from an experiment involving four levels of nitrogen (A), two times of planting (B), and two levels of potassium (C). Only one observation (N content, in percentage, of corn grain) was made for each of the 16 combinations of levels.
SSA = .22625 SSB = .000025 SSC = .0036 SSAB = .004325
SSAC = .00065 SSBC = .000625 SST = .2384.
a. Construct the ANOVA table.
b. Assume that there are no three-way interaction effects, so that MSABC is a valid estimate of
and test at level .05 for interaction and main effects.
c. The nitrogen averages are
Use Tukey's method to examine differences in percentage N among the nitrogen levels
(Essay)
4.8/5  (36)
(36)
The accompanying data resulted from a experiment with three replications per combination of treatments designed to study the effects of concentration of detergent (A), concentration of sodium carbonate (B), and concentration of sodium carboxymethyl cellulose (C0 on cleaning ability of a solution in washing tests (a larger number indicates better cleaning ability than a smaller number). Factor Levels A B C Condition Observations 1 1 1 (1) 106,93, 116 2 1 1 a 198,200,214 1 2 1 b 197,202,185 2 2 1 ab 329,331,307 1 1 2 c 149,169,135 2 1 2 ac 243,247,220 1 2 2 bc 255,230,252 2 2 2 abc 383,360,364
a. After obtaining cell totals 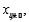 compute estimates of
b. Use the cell totals along with Yate's method to compute the effect contrasts and sums of squares. Then construct an ANOVA table and test all appropriate hypotheses using
compute estimates of
b. Use the cell totals along with Yate's method to compute the effect contrasts and sums of squares. Then construct an ANOVA table and test all appropriate hypotheses using
(Essay)
4.8/5  (37)
(37)
In a two-factor experiment where factor A consists of I levels, factor B consists of J levels, and there is only one observation on each of the IJ treatments, SST has __________ degrees of freedom.
(Short Answer)
4.8/5  (40)
(40)
Answer the following questions:
a. In a
experiment, suppose two blocks are to be used, and it is decided to confound the ABCD interaction with the block effect. Which treatments should be carried out in the first block [containing the treatment (1)], and which treatments are allocated to the second block?
b. In an experiment to investigate niacin retention in vegetables as a function of cooking temperature (A), sieve size (B), type of processing (C), and cooking time (D), each factor was held at two levels. Two blocks were used, with the allocation of blocks as given in part (a) to confound only the ABCD interaction with blocks. Use Yate's procedure to obtain the ANOVA table for the accompanying data. ![Answer the following questions: a. In a 2 ^ { 4 } experiment, suppose two blocks are to be used, and it is decided to confound the ABCD interaction with the block effect. Which treatments should be carried out in the first block [containing the treatment (1)], and which treatments are allocated to the second block? b. In an experiment to investigate niacin retention in vegetables as a function of cooking temperature (A), sieve size (B), type of processing (C), and cooking time (D), each factor was held at two levels. Two blocks were used, with the allocation of blocks as given in part (a) to confound only the ABCD interaction with blocks. Use Yate's procedure to obtain the ANOVA table for the accompanying data. c. Assume that all three-way interaction effects are absent, so that the associated sums of squares Can be combined to yield an estimate of \sigma ^ { 2 } and carry out all appropriate test at level .05.](https://storage.examlex.com/TB3498/11eb0e05_3eb3_fb82_9431_45cf96f48acd_TB3498_00.jpg) c. Assume that all three-way interaction effects are absent, so that the associated sums of squares
Can be combined to yield an estimate of
and carry out all appropriate test at level .05.
c. Assume that all three-way interaction effects are absent, so that the associated sums of squares
Can be combined to yield an estimate of
and carry out all appropriate test at level .05.
(Essay)
4.9/5  (36)
(36)
The accompanying data table gives observations on total acidity of coal samples of three different types, with determinations made using three different concentrations of ethanolic NaOH.
Type of Coal Morwell Yalloum Maddingley .404 8.27,8.17 8.66,8.61 8.14,7.96 NaOH Conc. .626 8.03,8.21 8.42,8.58 8.02,7.89 .786 8.60,8.20 8.61,8.76 8.13,8.07 Additionally,
a. Assuming both effects to be fixed, construct an ANOVA table, test for the presence of
ANOVA table, test for the presence of interaction, and then test for the presence of main effects for each factor (all using level .01).
b. Use Tukey's procedure to identify significant differences among the types of coal.
(Essay)
4.9/5  (35)
(35)
In a two-factor ANOVA problem, there are 4 levels of factor A, 5 levels of factor B, and 2 observations (replications) for each combination of levels of the two factors. Then, the number of treatments in this experiment is
(Multiple Choice)
4.9/5  (46)
(46)
The following equation SST = SSA + SSB + SSC + SSE applies to which ANOVA model?
(Multiple Choice)
4.7/5  (44)
(44)
Showing 1 - 20 of 62
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)