Exam 15: Multiple Regression
Exam 1: Data and Statistics84 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Displays67 Questions
Exam 3: Descriptive Statistics: Numerical Measures118 Questions
Exam 4: Introduction to Probability94 Questions
Exam 5: Discrete Probability Distributions84 Questions
Exam 6: Continuous Probability Distributions121 Questions
Exam 7: Sampling and Sampling Distributions116 Questions
Exam 8: Interval Estimation90 Questions
Exam 9: Hypothesis Tests95 Questions
Exam 10: Inference About Means and Proportions With Two Populations63 Questions
Exam 11: Inferences About Population Variances66 Questions
Exam 12: Comparing Multiple Proportions, Tests of Independence and Goodness of Fit59 Questions
Exam 13: Experimental Design and Analysis of Variance76 Questions
Exam 14: Simple Linear Regression132 Questions
Exam 15: Multiple Regression103 Questions
Exam 16: Regression Analysis: Model Building41 Questions
Exam 17: Time Series Analysis and Forecasting51 Questions
Exam 18: Nonparametric Methods58 Questions
Exam 19: Decision Analysis48 Questions
Exam 20: Index Numbers39 Questions
Exam 21: Statistical Methods for Quality Control60 Questions
Exam 22: Sample Survey48 Questions
Select questions type
A regression model between sales (y in $1000), unit price (x1 in dollars), and television advertisement (x2 in dollars) resulted in the following function: 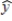 = 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20. To test for the significance of the model, the p-value is
= 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20. To test for the significance of the model, the p-value is
Free
(Multiple Choice)
4.8/5  (23)
(23)
Correct Answer:
A
A regression model between sales (y in $1000), unit price (x1 in dollars), and television advertisement (x2 in dollars) resulted in the following function: 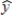 = 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20. To test for the significance of the model, the test statistic F is
= 8 - 4x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 20. To test for the significance of the model, the test statistic F is
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
A
For a multiple regression model, SST = 1000 and SSR = 800. The multiple coefficient of determination is
(Multiple Choice)
4.9/5  (39)
(39)
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 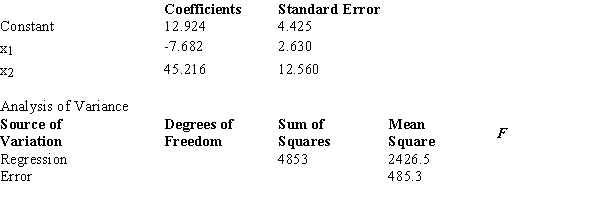 The sum of squares due to error (SSE) equals
The sum of squares due to error (SSE) equals
(Multiple Choice)
4.9/5  (32)
(32)
In a multiple regression model involving 60 observations, the following estimated regression equation was obtained: 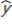 = 30 + 18x1 + 43x2 + 87x3+ 90x4
For this model, SSR = 800 and SST = 1400. MSR for this model is
= 30 + 18x1 + 43x2 + 87x3+ 90x4
For this model, SSR = 800 and SST = 1400. MSR for this model is
(Multiple Choice)
4.9/5  (39)
(39)
Below you are given a partial computer output from a multiple regression analysis based on a sample of 16 observations. 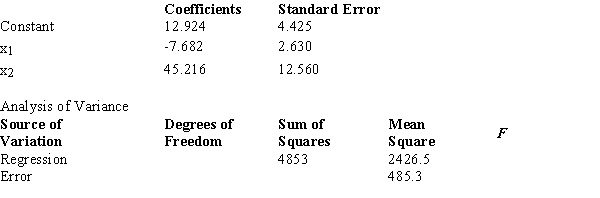 Carry out the test of significance for the parameter β1 at the 1% level. The null hypothesis should
Carry out the test of significance for the parameter β1 at the 1% level. The null hypothesis should
(Multiple Choice)
4.7/5  (33)
(33)
A regression model between sales (y in $1000), unit price (x1 in dollars), and television advertisement (x2 in dollars) resulted in the following function: 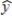 = 7 - 3x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 18. If we want to test for the significance of the regression model, the critical value of F at the 5% level of significance is
= 7 - 3x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 18. If we want to test for the significance of the regression model, the critical value of F at the 5% level of significance is
(Multiple Choice)
4.9/5  (42)
(42)
A regression model between sales (y in $1000), unit price (x1 in dollars), and television advertisement (x2 in dollars) resulted in the following function: 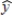 = 7 - 3x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 18. The multiple coefficient of determination for this problem is
= 7 - 3x1 + 5x2
For this model, SSR = 3500, SSE = 1500, and the sample size is 18. The multiple coefficient of determination for this problem is
(Multiple Choice)
4.9/5  (32)
(32)
In a multiple regression model involving 45 observations, the following estimated regression equation was obtained: 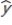 = 30 + 18x1 + 43x2 + 87x3+ 90x4
For this model, SSR = 800 and SST = 1400. Give degrees of freedom for the F critical value α = .05.
= 30 + 18x1 + 43x2 + 87x3+ 90x4
For this model, SSR = 800 and SST = 1400. Give degrees of freedom for the F critical value α = .05.
(Multiple Choice)
4.7/5  (39)
(39)
Even though a residual may be unusually large, the standardized residual rule might fail to identify the observation as being an outlier. This difficulty can be circumvented by using
(Multiple Choice)
4.8/5  (36)
(36)
In a multiple regression analysis, SSR = 1000 and SSE = 200. The multiple coefficient of determination is
(Multiple Choice)
4.7/5  (36)
(36)
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 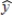 = 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384. From the above linear function for multiple regression, it can be said that the expected yearly income of
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384. From the above linear function for multiple regression, it can be said that the expected yearly income of
(Multiple Choice)
4.9/5  (32)
(32)
A multiple regression model has the following estimated form: 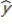 = 7 + 2x1 + 9x2
As x2 increases by 1 unit (holding x1 constant), y is expected to
= 7 + 2x1 + 9x2
As x2 increases by 1 unit (holding x1 constant), y is expected to
(Multiple Choice)
4.7/5  (38)
(38)
In a multiple regression model involving 50 observations, the following estimated regression equation was obtained: 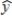 = 20 + 5x1 - 4x2 + 8x3 + 8x4
For this model, SSR = 700 and SSE = 100. The critical F value at α = .05 is (using the conservative value from the table)
= 20 + 5x1 - 4x2 + 8x3 + 8x4
For this model, SSR = 700 and SSE = 100. The critical F value at α = .05 is (using the conservative value from the table)
(Multiple Choice)
4.8/5  (37)
(37)
A term used to describe the case when the independent variables in a multiple regression model are correlated is
(Multiple Choice)
4.7/5  (39)
(39)
A regression model in which more than one independent variable is used to predict the dependent variable is called
(Multiple Choice)
4.7/5  (34)
(34)
The adjusted multiple coefficient of determination is adjusted for the
(Multiple Choice)
4.9/5  (27)
(27)
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female).
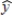 = 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384. At the 5% level, the model
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384. At the 5% level, the model
(Multiple Choice)
4.9/5  (35)
(35)
The following estimated regression equation was developed relating yearly income (y in $1000s) of 30 individuals with their age (x1) and their gender (x2) (0 if male and 1 if female). 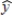 = 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384. The multiple coefficient of determination is
= 30 + .7x1 + 3x2
Also provided are SST = 1200 and SSE = 384. The multiple coefficient of determination is
(Multiple Choice)
4.8/5  (42)
(42)
Showing 1 - 20 of 103
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)