Question 1

The slope (b1) represents

Accepted Answer

A) predicted value of Y when X = 0. 
B) the estimated average change in Y per unit change in X. 
C) the predicted value of Y. 
D) variation around the line of regression. 
A) predicted value of Y when X = 0. 
B) the estimated average change in Y per unit change in X. 
C) the predicted value of Y. 
D) variation around the line of regression.

Question 2

SCENARIO 12-10
The management of a chain electronic store would like to develop a model for predicting the weekly sales (in thousands of dollars) for individual stores based on the number of customers who made purchases.A random sample of 12 stores yields the following results: $$\begin{array} { | l | c | } 
\hline \text { Customers } & \begin{array} { l } 
\text { Sales } \
\text { (Thousands of } \
\text { Dollars) }
\end{array} \
\hline 907 & 11.20 \
\hline 926 & 11.05 \
\hline 713 & 8.21 \
\hline 741 & 9.21 \
\hline 780 & 9.42 \
\hline 898 & 10.08 \
\hline 510 & 6.73 \
\hline 529 & 7.02 \
\hline 460 & 6.12 \
\hline 872 & 9.52 \
\hline 650 & 7.53 \
\hline 603 & 7.25 \
\hline
\end{array}$$
-Referring to Scenario 12-10, the p-value of the t test and F test should be the same when testing whether the number of customers who make purchases is a good predictor for weekly sales.

Accepted Answer

A) True 
 B)False

Question 3

SCENARIO 12-13
In this era of tough economic conditions, voters increasingly ask the question: "Is the educational achievement level of students dependent on the amount of money the state in which they reside spends on education?" The partial computer output below is the result of using spending per student ($) as the independent variable and composite score which is the sum of the math, science and reading scores as the dependent variable on 35 states that participated in a study.The table includes only partial results. $$\begin{array}{l}
\begin{array} { l c } 
\hline  { \text { Regression Statistics } } \
\hline \text { Multiple R } & 0.3122 \
\text { R Square } & 0.0975 \
\text { Adjusted R } & 0.0701 \
\text { Square } & \
\text { Standard } & 26.9122 \
\text { Error } & \
\text { Observations } & 35 \
\hline
\end{array}\\end{array}$$
 ANOVA 
$\begin{array}{lccc}
& d f & S S & M S & F \
\text { Regression } & 1 & 2581.5759 & \
\text { Residual } & & & 724.2674 \
\text { Total } & 34 & 26482.4000 &
\end{array}$
$$\begin{array}{l}\begin{array} { l c c c c } 
\hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & P \text {-value } \
\hline \text { Intercept } & 595.540251 & 22.115176 & & \
\text { Spending per } & & & & \
\text { Student(\$) } & 0.007996 & 0.004235 & \
\hline
\end{array}
\end{array}$$
-Referring to Scenario 12-13, the conclusion on the test of whether spending per student affects composite score using a 5% level of significance is

Accepted Answer

A) There is not enough evidence that spending per student affects composite score. 
B) There is enough evidence that spending per student affects composite score. 
C) There is not enough evidence that spending per student does not affect composite score. 
D) There is enough evidence that spending per student does not affect composite score. 
A) There is not enough evidence that spending per student affects composite score. 
B) There is enough evidence that spending per student affects composite score. 
C) There is not enough evidence that spending per student does not affect composite score. 
D) There is enough evidence that spending per student does not affect composite score.

Question 4

SCENARIO 12-5
The managing partner of an advertising agency believes that his company's sales are related to the industry sales.He uses Microsoft Excel to analyze the last 4 years of quarterly data with the following results: $\begin{array}{ll}
{\text { Regression Statistics }} \
\text { Multiple R } & 0.802 \
\text { R Square } & 0.643 \
\text { Adjusted R Square } & 0.618 \
\text { Standard Error Syv } & 0.9234\
\text { Observations } & 16
\end{array}$
ANOVA
$\begin{array}{lrrrcc} 
& \text { df } & \text { SS } & \text { MS } & \text { F } & \text { Sig.F } \
\text { Regression } & 1 & 21.497 & 21.497 & 25.27 & 0.000 \
\text { Error } & 14 & 11.912 & 0.851 & & \
\text { Total } & 15 & 33.409 & & &
\end{array}$

$\begin{array}{llll}\text { Predictor Coef } & \text { StdError } t \text { Stat } & \text { P-value }\
\hline\text { Intercept }& 3.962 & 1.440 & 2.75 & 0.016 \
\text { Industry } &0.040451 & 0.008048 & 5.03 & 0.000
\end{array}$

$\text { Durbin-Watson Statistic } \quad 1.59$
-Referring to Scenario 12-5, the coefficient of determination is _.

Accepted Answer

The answer of SCENARIO 12-5
The managing partner of an advertising...

Question 5

SCENARIO 12-9
It is believed that, the average numbers of hours spent studying per day (HOURS) during undergraduate education should have a positive linear relationship with the starting salary (SALARY, measured in thousands of dollars per month) after graduation.Given below is the Excel output for predicting starting salary (Y) using number of hours spent studying per day (X) for a sample of 51 students.NOTE: Only partial output is shown. $\begin{array}{lr}
{\text { Regression Statistics }} \
\hline \text { Multiple R } & 0.8857 \
\text { R Square } & 0.7845 \
\text { Adjusted R Square } & 0.7801 \
\text { Standard Error } & 1.3704 \
\text { Observations } & 51 \
\hline
\end{array}$
ANOVA
$\begin{array}{lrrrrr} 
& d f & S S & M S & F & \text { Significance F } \
\hline \text { Regression } &  1 & 335.0472 & 335.0473 & 178.3859 \
\text { Residual } & & &  1.8782 & \
\text { Total } & 50 & 427.0798 & &
\end{array}$

$\begin{array}{lrrrrrrr} 
& \text { Coefficients } & \text { standered Error } & \text { tStat } & \text { P-value } & \text { Lower 95\% } & \text { Upper 95\% } \
\hline \text { Intercept } & -1.8940 & 0.4018 & -4.7134 & 0.0000 & -2.7015 & -1.0865 \
\text { Hours } & 0.9795 & 0.0733 & 13.3561 & 0.0000 & 0.8321 & 1.1269
\end{array}$ Note: 2.051E - 05 = 2.051 *10-05 and 5.944 E - 18 = 5.944 *10-18 .
-Referring to Scenario 12-9, the error sum of squares (SSE) of the above regression is

Accepted Answer

A) 1.878215 
B) 92.0325465 
C) 335.047257 
D) 427.079804 
A) 1.878215 
B) 92.0325465 
C) 335.047257 
D) 427.079804

Question 6

SCENARIO 12-11
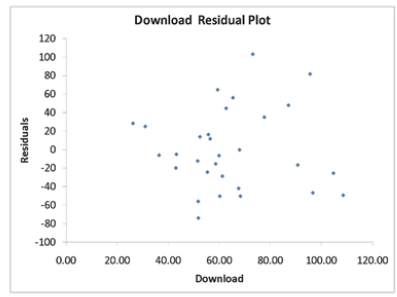
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression
along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
   $\begin{array}{lr}
{\text { Regression Statistics }} \
\hline \text { Multiple R } & 0.8691 \
\hline \text { R Square } & 0.7554 \
\hline \text { Adjusted R Square } & 0.7467 \
\hline \text { Standard Error } & 44.4765 \
\hline \text { Observations } & 30.0000 \
\hline
\end{array}$

$\text { ANOVA }$ 
$\begin{array}{|l|r|r|r|r|r|}
\hline &\text { df } & \text { SS } & \text { MS } & F & \text { Significance } F \ 
\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \
\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \
\hline \text { Total } & 29 & 226451.3503 & & \
\hline
\end{array}$

Simple Linear Regression 12-41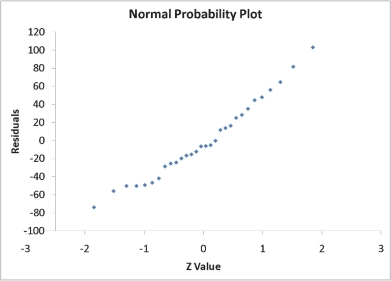  
-Referring to Scenario 12-11, what is the standard error of estimate?

Accepted Answer

The answer of SCENARIO 12-11
A computer software developer would like...

Question 7

The sample correlation coefficient between X and Y is 0.375.It has been found out that the p- value is 0.744 when testing H0 : $\rho$ = 0 against the one-sided alternative H1 : $\rho$ $\lt$ 0 .To testH0 : $\rho$=0 against the two-sided alternative H1 : $\rho$$\neq$ 0 at a significance level of 0.1, the p-value is

Accepted Answer

A) 0.744 / 2 
B) (0.744)(2) 
C) 1- 0.744 
D) (1- 0.744)(2) 
A) 0.744 / 2 
B) (0.744)(2) 
C) 1- 0.744 
D) (1- 0.744)(2)

Question 8

SCENARIO 12-4
The managers of a brokerage firm are interested in finding out if the number of new clients a broker brings into the firm affects the sales generated by the broker.They sample 12 brokers and determine the number of new clients they have enrolled in the last year and their sales amounts in thousands of dollars.These data are presented in the table that follows. $\begin{array}{lll}
\text { Broker } & \text {Clients} & \text {Sales }\
1 & 27 & 52 \
2 & 11 & 37 \
3 & 42 & 64 \
4 & 33 & 55 \
5 & 15 & 29 \
6 & 15 & 34 \
7 & 25 & 58 \
8 & 36 & 59 \
9 & 28 & 44 \
10 & 30 & 48 \
11 & 17 & 31 \
12 & 22 & 38
\end{array}$
-Referring to Scenario 12-4, suppose the managers of the brokerage firm want to construct a 99%confidence interval estimate for the mean sales made by brokers who have brought into the firm24 new clients.The confidence interval is from to .

Accepted Answer

The answer of SCENARIO 12-4
The managers of a brokerage firm...

Question 9

SCENARIO 12-10
The management of a chain electronic store would like to develop a model for predicting the weekly sales (in thousands of dollars) for individual stores based on the number of customers who made purchases.A random sample of 12 stores yields the following results: $$\begin{array} { | l | c | } 
\hline \text { Customers } & \begin{array} { l } 
\text { Sales } \
\text { (Thousands of } \
\text { Dollars) }
\end{array} \
\hline 907 & 11.20 \
\hline 926 & 11.05 \
\hline 713 & 8.21 \
\hline 741 & 9.21 \
\hline 780 & 9.42 \
\hline 898 & 10.08 \
\hline 510 & 6.73 \
\hline 529 & 7.02 \
\hline 460 & 6.12 \
\hline 872 & 9.52 \
\hline 650 & 7.53 \
\hline 603 & 7.25 \
\hline
\end{array}$$
-Referring to Scenario 12-10, what is the value of the standard error of the estimate?

Accepted Answer

The answer of SCENARIO 12-10
The management of a chain electronic...

Question 10

SCENARIO 12-4
The managers of a brokerage firm are interested in finding out if the number of new clients a broker brings into the firm affects the sales generated by the broker.They sample 12 brokers and determine the number of new clients they have enrolled in the last year and their sales amounts in thousands of dollars.These data are presented in the table that follows. $\begin{array}{lll}
\text { Broker } & \text {Clients} & \text {Sales }\
1 & 27 & 52 \
2 & 11 & 37 \
3 & 42 & 64 \
4 & 33 & 55 \
5 & 15 & 29 \
6 & 15 & 34 \
7 & 25 & 58 \
8 & 36 & 59 \
9 & 28 & 44 \
10 & 30 & 48 \
11 & 17 & 31 \
12 & 22 & 38
\end{array}$
-Referring to Scenario 12-4, the standard error of estimate is .

Accepted Answer

The answer of SCENARIO 12-4
The managers of a brokerage firm...

Question 11

14.Referring to Scenario 12-2, what is the standard error of the regression slope estimate, S ?
 $$b$$ 1
a) 0.784 b) 0.885 c) 12.650 d) 16.299
ANSWER:
c
TYPE: MC DIFFICULTY: Moderate
KEYWORDS: standard error, slope
-Referring to Scenario 12-2, if the price of the candy bar is set at $2, the estimated mean sales will be

Accepted Answer

A) 30 
B) 65 
C) 90 
D) 100 
A) 30 
B) 65 
C) 90 
D) 100

Question 12

SCENARIO 12-1
A large national bank charges local companies for using their services.A bank official reported the results of a regression analysis designed to predict the bank's charges (Y) -- measured in dollars per month -- for services rendered to local companies.One independent variable used to predict service charges to a company is the company's sales revenue (X) -- measured in millions of dollars.Data for
21 companies who use the bank's services were used to fit the model: $$Y _ { i } = \beta _ { 0 } + \beta _ { 1 } X _ { i } + \varepsilon _ { i }$$
Theresultsofthesimplelinearregressionareprovidedbelow.
$$\bar { I } = - 2,700 + 20 X , S _ { Z X } = 65 \text {, two-tail } p \text { value } = 0.034 \text { (for testing } \beta _ { 1 } \text { ) }$$
-Referring to Scenario 12-1, a 95% confidence interval for $\beta$1 is (15, 30).Interpret the interval.

Accepted Answer

A) You are 95% confident that the mean service charge will fall between $15 and $30 per month. 
B) You are 95% confident that the sales revenue (X)will increase between $15 and $30 million for every $1 increase in service charge (Y). 
C) You are 95% confident that mean service charge (Y)will increase between $15 and $30 for every $1 million increase in sales revenue (X). 
D) At the $\alpha$ = 0.05 level, there is no evidence of a linear relationship between service charge (Y)and sales revenue (X). 
A) You are 95% confident that the mean service charge will fall between $15 and $30 per month. 
B) You are 95% confident that the sales revenue (X)will increase between $15 and $30 million for every $1 increase in service charge (Y). 
C) You are 95% confident that mean service charge (Y)will increase between $15 and $30 for every $1 million increase in sales revenue (X). 
D) At the $\alpha$ = 0.05 level, there is no evidence of a linear relationship between service charge (Y)and sales revenue (X).

Question 13

If the Durbin-Watson statistic has a value close to 4, which assumption is violated?

Accepted Answer

A) Normality of the errors. 
B) Independence of errors. 
C) Homoscedasticity. 
D) None of the above. 
A) Normality of the errors. 
B) Independence of errors. 
C) Homoscedasticity. 
D) None of the above.

Question 14

The coefficient of determination represents the ratio of SSR to SST.

Accepted Answer

A) True 
 B)False

Question 15

SCENARIO 12-3
The director of cooperative education at a state college wants to examine the effect of cooperative education job experience on marketability in the work place.She takes a random sample of 4 students.For these 4, she finds out how many times each had a cooperative education job and how many job offers they received upon graduation.These data are presented in the table below. $\begin{array} {ccc}\text { Student } & \text { Coop Jobs  } & \text {Job Offer }\ 1 & 1 & 4 \ 2 & 2 & 6 \ 3 & 1 & 3 \ 4 & 0 & 1 \end{array}$
-Referring to Scenario 12-3, suppose the director of cooperative education wants to construct a95% confidence-interval estimate for the mean number of job offers received by students who have had exactly one cooperative education job.The t critical value she would use is _.

Accepted Answer

The answer of SCENARIO 12-3
The director of cooperative education at...

Question 16

SCENARIO 12-10
The management of a chain electronic store would like to develop a model for predicting the weekly sales (in thousands of dollars) for individual stores based on the number of customers who made purchases.A random sample of 12 stores yields the following results: $$\begin{array} { | l | c | } 
\hline \text { Customers } & \begin{array} { l } 
\text { Sales } \
\text { (Thousands of } \
\text { Dollars) }
\end{array} \
\hline 907 & 11.20 \
\hline 926 & 11.05 \
\hline 713 & 8.21 \
\hline 741 & 9.21 \
\hline 780 & 9.42 \
\hline 898 & 10.08 \
\hline 510 & 6.73 \
\hline 529 & 7.02 \
\hline 460 & 6.12 \
\hline 872 & 9.52 \
\hline 650 & 7.53 \
\hline 603 & 7.25 \
\hline
\end{array}$$
-Referring to Scenario 12-10, what is the value of the coefficient of correlation?

Accepted Answer

The answer of SCENARIO 12-10
The management of a chain electronic...

Question 17

SCENARIO 12-11
A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware.Following is the output from a simple linear regression
along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed:
   $\begin{array}{lr}
{\text { Regression Statistics }} \
\hline \text { Multiple R } & 0.8691 \
\hline \text { R Square } & 0.7554 \
\hline \text { Adjusted R Square } & 0.7467 \
\hline \text { Standard Error } & 44.4765 \
\hline \text { Observations } & 30.0000 \
\hline
\end{array}$

$\text { ANOVA }$ 
$\begin{array}{|l|r|r|r|r|r|}
\hline &\text { df } & \text { SS } & \text { MS } & F & \text { Significance } F \ 
\hline \text { Regression } & 1 & 171062.9193 & 171062.9193 & 86.4759 & 0.0000 \
\hline \text { Residual } & 28 & 55388.4309 & 1978.1582 & & \
\hline \text { Total } & 29 & 226451.3503 & & \
\hline
\end{array}$

Simple Linear Regression 12-41  
-Referring to Scenario 12-11, there appears to be autocorrelation in the residuals.

Accepted Answer

A) True 
 B)False

Question 18

SCENARIO 12-8
It is believed that GPA (grade point average, based on a four point scale) should have a positive linear relationship with ACT scores.Given below is the Excel output for predicting GPA using ACT scores based a data set of 8 randomly chosen students from a Big-Ten university.
Regressing GPA on ACT $$\begin{array}{l}
\begin{array} { l r } 
\hline  { \text { Regression Statistics } } \
\hline \text { Multiple R } & 0.7598 \
\text { R Square } & 0.5774 \
\text { Adjusted R Square } & 0.5069 \
\text { Standard Error } & 0.2691 \
\text { Qbservations } & 8 \
\hline
\end{array}\\end{array}$$
ANOVA 
$\begin{array}{lrrrcc} 
\hline & \text { df } & \text { SS } & \text { MS } & \text { F } & \text { Significance.F } \
\hline\text { Regression } & 1 & 0.5940&0.5940&8.1986&0.0286 \
\text { Error } & 6 & 0.4347&0.0724\
\text { Total } & 7 &1.0287\\hline
\end{array}$
$$\begin{array}{l}\begin{array} { l c r r r r r } 
\hline & \text { Coefficients } & \text { Standard Error } & t \text { Stat } & P \text {-value } & \text { Lower 95\% } & \text { Upper 95\% } \
\hline \text { Intercept } & 0.5681 & 0.9284 & 0.6119 & 0.5630 & - 1.7036 & 2.8398 \
\text { ACT } & 0.1021 & 0.0356 & 2.8633 & 0.0286 & 0.0148 & 0.1895 \
\hline
\end{array}
\end{array}$$
-Referring to Scenario 12-8, the interpretation of the coefficient of determination in this regression is

Accepted Answer

A) 57.74% of the total variation of ACT scores can be explained by GPA. 
B) ACT scores account for 57.74% of the total fluctuation in GPA. 
C) GPA accounts for 57.74% of the variability of ACT scores. 
D) None of the above. 
A) 57.74% of the total variation of ACT scores can be explained by GPA. 
B) ACT scores account for 57.74% of the total fluctuation in GPA. 
C) GPA accounts for 57.74% of the variability of ACT scores. 
D) None of the above.

Question 19

SCENARIO 12-4
The managers of a brokerage firm are interested in finding out if the number of new clients a broker brings into the firm affects the sales generated by the broker.They sample 12 brokers and determine the number of new clients they have enrolled in the last year and their sales amounts in thousands of dollars.These data are presented in the table that follows. $\begin{array}{lll}
\text { Broker } & \text {Clients} & \text {Sales }\
1 & 27 & 52 \
2 & 11 & 37 \
3 & 42 & 64 \
4 & 33 & 55 \
5 & 15 & 29 \
6 & 15 & 34 \
7 & 25 & 58 \
8 & 36 & 59 \
9 & 28 & 44 \
10 & 30 & 48 \
11 & 17 & 31 \
12 & 22 & 38
\end{array}$
-Referring to Scenario 12-4, suppose the managers of the brokerage firm want to construct both a99% confidence interval estimate and a 99% prediction interval for X = 24.The confidence interval estimate would be the (wider or narrower) of the two intervals.

Accepted Answer

The answer of SCENARIO 12-4
The managers of a brokerage firm...

Question 20

In a simple linear regression problem, r and b1

Accepted Answer

A) may have opposite signs. 
B) must have the same sign. 
C) must have opposite signs. 
D) are equal. 
A) may have opposite signs. 
B) must have the same sign. 
C) must have opposite signs. 
D) are equal.

The slope (b1) represents

If the Durbin-Watson statistic has a value close to 4, which assumption is violated?

The coefficient of determination represents the ratio of SSR to SST.

In a simple linear regression problem, r and b1

Defining and Collecting Data

Organizing and Visualizing Variables

Numerical Descriptive Measures

Basic Probability

Discrete Probability Distributions

The Normal Distribution

Sampling Distributions

Confidence Interval Estimation

Fundamentals of Hypothesis Testing: One-Sample Tests

Two-Sample Tests

Chi-Square Tests

Multiple Regression

Business Analytics

Filters

Exam 12: Simple Linear Regression

The slope (b1) represents

If the Durbin-Watson statistic has a value close to 4, which assumption is violated?

The coefficient of determination represents the ratio of SSR to SST.

In a simple linear regression problem, r and b1

Defining and Collecting Data

Organizing and Visualizing Variables

Numerical Descriptive Measures

Basic Probability

Discrete Probability Distributions

The Normal Distribution

Sampling Distributions

Confidence Interval Estimation

Fundamentals of Hypothesis Testing: One-Sample Tests

Two-Sample Tests

Chi-Square Tests

Multiple Regression

Business Analytics

Filters