Exam 12: Statistical Analysis Questions in ANOVA and Rank-Sum Test

In a study of reaction times, the time to respond to a visual stimulus (x)and the

The following display from a TI-84 Plus calculator presents the results of a test of the null hypothesis $H _ { 0 } : \beta _ { 1 } = 0$ . What is the P-value?

Monthly rents were recorded for a sample of 36 apartments in a certain city. The results were as follows. 1180 1240 1170 1280 1040 980 1420 1150 1060 990 1010 1260 1350 1130 1370 1130 990 1080 1220 1420 1130 1050 1130 1090 1030 1260 1030 1170 1050 1320 1450 1000 1090 1450 1120 1120 Can you conclude that the median rent is less than $\$ 1200$ per month? Use the $\alpha = 1$ level of significance. a. State appropriate null and alternate hypotheses. b. Compute the test statistic. c. Find the critical value. d. State a conclusion. were as follows.

Artificial hip joints consist of a ball and socket. As the joint wears, the ball (head) becomes rough. Investigators performed wear tests on metal, artificial hip joints. Joints with several different diameters were tested. The following table presents measurements of head roughness (in nanometers). Diameter Head Roughness 16 20.9 20.0 31.4 24.8 24 32.6 28.0 36.5 30 19.0 19.3 29.8 i). Construct an ANOVA table. ii). Can you conclude that the mean roughness varies with diameter? Use the $\alpha = \mathrm { C }$ level of significance.

The following data was collected as part of a study examining whether there is a difference between the number of hours men and women watch television. The values represent the number of hours a subject watched television on a designated Tuesday night. In the process of computing the test value the data from both samples should be combined, arranged in order, and ranked according to each group. Calculate the sum of the ranks for both groups. Lower values rank ahead of higher ones Men 2.0 1.5 3.0 2.5 2.0 1.0 0.0 2.0 1.5 2.5 2.0 2.0 Women 2.0 2.5 1.0 1.0 1.5 2.5 2.0 1.0 2.0 1.5 1.0 0.0

What is the critical value? The summary statistics for a certain set of points are: $n = 16 , s _ { \mathrm { e } } = 2.638$ , $\sum ( x - \bar { x } ) ^ { 2 } = 17.094$ , and $b _ { 1 } = 1.408$ . Assume the conditions of the linear model hold. A $99 \%$ confidence interval for $\beta _ { 1 }$ will be constructed.

In a water-bottling facility, several machines fill plastic bottles with 16 ounces of drinking water. The following TI-84 Plus display presents the results of a one-way ANOVA to determine whether the mean fill volumes differ among the filling machines 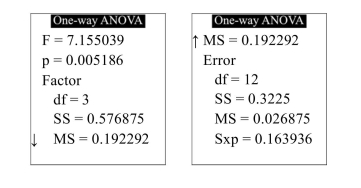Can you conclude that the mean fill volume differs among the filling machines? Use the $c$ level of significance.

Artificial hip joints consist of a ball and socket. As the joint wears, the ball (head) becomes rough. Investigators performed wear tests on metal artificial; hip joints. Joints with several different diameters were tested. The following table presents measurements of head roughness (in nanometers). Diameter Head Roughness 16 19.8 25.9 17.5 23.2 24 31.9 33.0 27.7 30 26.6 28.8 21.2 Perform the Tukey-Kramer test to determine which pairs of means, if any, differ. Use the $\alpha = 0.05$ level of significance.

Following is a set of observed and expected frequencies: ) Observed 5 18 26 23 16 Expected 10 15 30 15 10 Test the hypothesis that the distribution of the observed frequencies is as given by the expected frequencies. Use the $\alpha = 0.05$ level of significance.

Samples were drawn from three populations. The sample sizes were $n _ { 1 } = 7 , n _ { 2 } = 7$ and $n _ { 3 } = 5$ The sample means were $\bar { x } _ { 1 } = 1.27 , \bar { x } _ { 2 } = 1.99 \text {, and } \bar { x } _ { 3 } = 1.49 \text {. }$ The sample standard deviations were $s _ { 1 } = 0.25 , s _ { 2 } = 0.28 , \text { and } s _ { 3 } = 0.25$ The grand mean is $\bar { x } = 1.593158$ How many degrees of freedom are there for SSTr.

An experiment is conducted to study the effects of curing times and curing temperatures on the bonding strength of an epoxy adhesive. In the experiment, two steel rods are adhered together end-to-end, and the bonding strength is defined as the force, in pounds, required to pull the bond apart. For each combination of curing time and curing temperature, three tests are performed. The results of the experiment are shown below. Can the main effect of curing temperature (low or high) on bonding strength be interprete interpret the main effect using the $\alpha = 0.05$ level of significance.

In a study of reaction times,) Visual Auditory 208 249 200 244 245 254 234 249 155 243 211 248 189 244 206 247 Test $H _ { 0 } : \beta _ { 1 } = 0$ versus $H _ { 1 } : \beta _ { 1 } \neq 0$ . Use the $\alpha = 0.05$ level of significance.

A psychology instructor gave a five-question true-false quiz to her class of 171

Samples were drawn from three populations. The sample sizes were $n _ { 1 } = 5 , n _ { 2 } = 7$ and $n _ { 3 } = 5$ The sample means were $\bar { x } _ { 1 } = 1.43 , \bar { x } _ { 2 } = 1.85 , \text { and } \bar { x } _ { 3 } = 1.38$ The sample standard deviations were $s _ { 1 } = 0.31 , s _ { 2 } = 0.40 , \text { and } s _ { 3 } = 0.38$ The grand mean is $\overline { \bar { x } } = 1.588235$ Compute the mean squares MSE.

The following table shows the weekly total sales (in dollars) at a small roadside vegetable stand for the months June through September Month Weekly Sales June 980 1096 1103 869 July 1061 1042 929 1014 August 1060 1176 1447 1130 September 1018 872 986 1103 Can you conclude that the weekly sales varies with the month? Use the $\alpha = 0.05$ level of significance.

The sign test is performed to test $H _ { 0 } : m = 32 \text { versus } H _ { 1 } : m < 32$ There are 17 positive signs and 21 negative signs in a test involving 38 samples. What is the value of the test statistic?

Fill in the blank with the appropriate word or phrase. The null hypothesis for the rank-sum test is that the two population ? are equal

In a water-bottling facility, several machines fill plastic bottles with 16 ounces of drinking water. The following TI-84 Plus display presents the results of a one-way ANOVA to determine whether the mean fill volumes differ among the filling machines What is the value of MSE?

Given $n _ { 1 } = 14 , n _ { 2 } = 22 , \mathrm {~S} = 205 , \text { and } H _ { 1 } : m _ { 1 } < m _ { 2 }$ find the P -value.

The following MINITAB output presents a multiple regression equation $\hat { y } = b _ { 0 } + b _ { 1 } x _ { 1 } +$ $b _ { 2 } x _ { 2 } + b _ { 3 } x _ { 3 } + b _ { 4 } x _ { 4 }$ The regression equation is $\mathrm { Y } = 5.3535 + 0.7929 \mathrm { X } 1 - 0.8918 \mathrm { X } 2 + 0.5297 \mathrm { X } 3 - 1.7948 \mathrm { X } 4$ Predictor Coef SE Coef T P Constant 5.3535 0.7240 0.8771 0.338 X1 0.7929 0.7986 3.3073 0.002 X2 -0.8918 0.8208 -2.9354 0.009 X3 0.5297 0.8980 1.9458 0.083 X4 -1.7948 0.6461 -1.0262 0.340 $\mathrm{S}=2.2300 \quad \mathrm{R}-\mathrm{Sq}=50.0 \% \quad \mathrm{R}-\mathrm{Sq}(\mathrm{adj})=42.3 \%$ Analysis of Variance Source DF SS MS F P Regression 4 1188.8 297.2 7.7396 0.003 Residual Error 31 1190.1 38.4 Total 35 2378.9 What percentage of the variation in y is explained by the model?