Exam 8: Sequences, Series, Induction, and Probability

Solve the problem. -A basketball player makes approximately 69% of free throws. If she plays in a game in which she shoots 7 free throws, what is the probability the she will make all 7?

Solve the problem. -The final exam grades for a sample of students in a physical science class resulted in the following grade distribution. 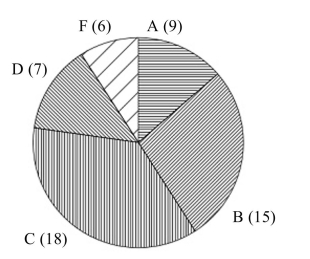If one student taking physical science is selected at random, find the probability of the following events. a. The student earned an "A". b. The student earned an "F".

Rewrite the series as an equivalent series with the new index of summation. - $\sum _ { i = 1 } ^ { 7 } ( 9 i ) = \sum _ { k = 3 } ^ { ? } ( ? )$

Solve the problem. -A physical activity class requires students to jog around an indoor track. For the first week of class the students jog 300 m around the track each day. Each week thereafter, the students increase the Distance jogged by 125 m. Write the nth term of a sequence defining the number of meters joggedBEach day by the students in the nth week of class.

Solve the problem. -The 5-yr survival rate for a type of cancer is 84%. If two people with this type of cancer are selected at random, what is the probability that they both survive 5 yr?

Write the first four terms of an arithmetic sequence, $\left\{ a _ { n } \right\}$ , based on the given information about the sequence. - $a _ { 1 } = 3 , d = 6$

For the expression ________ $n \geq 1$ represents the product of the first n positive integers $n(n-1)(n-2) \cdots(2)(1)$ , For n = 0 we have 0!= ________

Solve the problem. -Expenses for a company for year 1 are $\$ 20,000$ . Every year thereafter, expenses increase by $\$ 1,500$ plus $2 \%$ of the cost of the prior year. Let $a _ { 1 }$ represent the original cost for year 1 ; that is $a _ { 1 } = 20,000$ . Use a recursive formula to find the cost $a _ { n }$ in terms of $a _ { n - 1 }$ for each subsequent year, $\mathrm { n } \geq 2$ .

Solve the problem. -A certain city has approximately 2.75 million people. A census indicated that 450,000 people in the city were over the age of 60. If a person is selected at random from the city, what is the probability That the person is over 60 years old? Round to 3 decimal places.

Write the first five terms of the sequence defined recursively. - $a _ { 1 } = 6 , a _ { n } = - \frac { 1 } { a _ { n - 1 } }$

Find the indicated term of the arithmetic sequence based on the given information. - $a _ { 17 } = 9.76$ and $a _ { 41 } = 10.72 ;$ Find $a _ { 108 }$

Find the indicated term of a geometric sequence from the given information. - $a _ { n } = - 4 ( 2 ) ^ { n - 1 }$ , find $a _ { 4 }$

Use mathematical induction to prove the given statement for all positive integers n and real numbers x and y. - $\text { If } x < 1 \text {, then } x ^ { n } > x ^ { n - 1 } \text {. }$

Evaluate the sum. - $\sum _ { k = 1 } ^ { 158 } \left( 7 - \frac { 1 } { 4 } k \right)$

Find the indicated term of a geometric sequence from the given information. - $a _ { 5 } = \frac { 81 } { 16 }$ and $r = - \frac { 3 } { 4 }$ . Find $a _ { 1 }$ .

Solve the problem. -A student studying to be a veterinarian's assistant keeps track of a kitten's weight each week for a 5-week period after birth. Week number 12345 Weight (lb) 0.7 0.97 1.24 1.51 1.78 a. Write an expression for the nth term of the sequence representing the kitten's weight, n weeks after birth. b. If the weight of the kitten continues to increase linearly for 3 months, predict the kitten's weight 10 weeks After birth.

Write a recursive formula to define the sequence. - $a _ { 1 } = 2 , d = - 9$

Expand the binomial by using the binomial theorem. - $( 0.2 a + 0.5 b ) ^ { 4 }$

Write the sum using summation notation. - $4 + 4 + 4 + 4 + 4 + 4$

Choose the one alternative that best completes the statement or answers the question. Determine whether the sequence is geometric. If so, find the value of r. - $\frac { 6 } { t ^ { 2 } } , \frac { 9 } { t ^ { 4 } } , \frac { 12 } { t ^ { 6 } } , \frac { 15 } { t ^ { 8 } }$