Exam 5: Probability

There are 32 chocolates in a box, all identically shaped. There 11 are filled with nuts, 8 with caramel, and 13 aresolid chocolate. You randomly select one piece, eat it, and then select a second piece. Find the probability ofselecting 2 nut candies.

Use the spinner below to answer the question. Assume that it is equally probable that the pointer will land onany one of the five numbered spaces. If the pointer lands on a borderline, spin again. 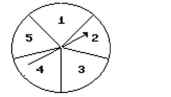Find the probability that the arrow will land on an odd number.

Amy, Jean, Keith, Tom, Susan, and Dave have all been invited to a birthday party. They arrive randomly andeach person arrives at a different time. In how many ways can they arrive? In how many ways can Jean arrivefirst and Keith last? Find the probability that Jean will arrive first and Keith will arrive last.

An ice chest contains 4 cans of apple juice, 8 cans of grape juice, 6 cans of orange juice, and 5 cans of pineapplejuice. Suppose that you reach into the container and randomly select three cans in succession. Find theprobability of selecting no grape juice.

True or False: If A and B are independent events, then A and B are mutually exclusive also.

Suppose that there are two buckets. Bucket 1 contains 3 tennis balls and 5 ping -pong balls. Bucket 2 contains 4tennis balls, 3 ping-pong balls, and 5 baseballs. An unfair coin will decide from which bucket we draw. Headsimplies we draw from Bucket 1 and tails implies we draw from Bucket 2. The probability of a heads is 13 andthe probability of a tails is $\frac { 2 } { 3 } .$ Given that a ping-pong ball was selected what is the probability that it camefrom Bucket 2?

A church has 8 bells in its bell tower. Before each church service 3 bells are rung in sequence. No bell is rungmore than once. How many sequences are there?

The probability that event A will occur is $\mathrm { P } ( \mathrm { A } ) = \frac { \text { Number of successful outcomes } } { \text { Number of unsuccessful outcomes } }$

Given that events A and B are mutually exclusive and P(A) = 0.5 and P(B) = 0.7, are A and B independent?

The manager of a used car lot took inventory of the automobiles on his lot and constructed the following tablebased on the age of his car and its make (foreign or domestic). A car was randomly selected from the lot. Giventhat the car selected was a domestic car, what is the probability that it was older than 2 years? Age of Car (in years) Make 0-2 3-5 6-10 over 10 Total Foreign 40 30 10 20 100 Domestic 45 27 11 17 100 Total 85 57 21 37 200

A company manufactures shoes in three different factories. Factory Omaha Produces 25% of the companyʹsshoes, Factory Chicago produces 60%, and factory Seattle produces 15%. One percent of the shoes produced inOmaha are mislabeled, 0.5 % of the Chicago shoes are mislabeled, and 2% of the Seattle shoes are mislabeled.If you purchase one pair of shoes manufactured by this company what is the probability that it was labeledcorrectly?

You are dealt one card from a standard 52-card deck. Find the probability of being dealt a picture card.

A probability experiment is conducted in which the sample space of the experiment is S={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15} . Let event A={7,8,9,10} and event B={9,10,11,12,13} . Assume that each outcome is equally likely. List the outcomes in A or B. Find P(A or B).

A fair coin is tossed two times in succession. The set of equally likely outcomes is {HH, HT, TH, TT}. Find theprobability of getting the same outcome on each toss.

Suppose that events E and F are independent, P(E) = 0.8 and P(F ) = 0.9. What is the P(E and F )?

You want to arrange 12 of your favorite CDʹs along a shelf. How many different ways can you arrange theCDʹs assuming that the order of the CDʹs makes a difference to you?

How many distinct arrangements of the letters in the word football are possible?

There are 6 performers who are to present their acts at a variety show. How many different ways are there toschedule their appearances?

A bag contains 10 white, 12 blue, 13 red, 7 yellow, and 8 green wooded balls. A ball is selected from the bag, itscolor noted, then replaced. You then draw a second ball, note its color and then replace the ball. What is theprobability of selecting 2 red balls? Round to the nearest ten-thousandth.

The table lists the drinking habits of a group of college students. If a student is chosen at random, find theprobability of getting someone who is a man or a woman. Round your answer to three decimal places. Sex Non-drinker Regular Drinker Heavy Drinker Total Man 135 58 5 198 Woman 187 21 8 216 Total 322 79 13 414