Exam 3: Logic
Exam 1: Critical Thinking Skills95 Questions
Exam 2: Sets126 Questions
Exam 3: Logic201 Questions
Exam 4: Systems of Numeration162 Questions
Exam 5: Number Theory and the Real Number System197 Questions
Exam 7: Algebra, Graphs, and Functions188 Questions
Exam 8: The Metric System188 Questions
Exam 9: Geometry147 Questions
Exam 10: Consumer Mathematics221 Questions
Exam 11: Probability309 Questions
Exam 14: Voting and Apportionment71 Questions
Select questions type
Convert the compound statement into words.
- = "The food tastes delicious." = "We eat a lot." = "Nobody has dessert." \sim\vee(\wedge)
(Multiple Choice)
4.8/5  (33)
(33)
Determine the truth value for each simple statement. Then, using the truth values, give the truth value of the compound statement.
-
(True/False)
4.9/5  (36)
(36)
Determine the truth value for the simple statement. Then use these truth values to determine the truth value of the compound statement. Use the chart or graph when provided.
-9 + 6 = 20 - 5 and 48 ÷ 4 = 4 ∙ 3
(True/False)
4.8/5  (36)
(36)
Use truth tables to test the validity of the argument.
- \rightarrow\sim \sim\sim \therefore\vee
(Multiple Choice)
4.8/5  (31)
(31)
Determine which, if any, of the three statements are equivalent.
-I. If tomorrow is not Monday, then today is not Sunday.
II. Today is not Sunday and tomorrow is not Monday.
III. It is not the case that today is Sunday and tomorrow is Monday.
(Multiple Choice)
4.9/5  (28)
(28)
Let p represent the statement, ʺJim plays footballʺ, and let q represent ʺMichael plays basketballʺ. Convert the compound statements into symbols.
-Neither Jim plays football nor Michael plays basketball.
(Multiple Choice)
4.9/5  (38)
(38)
Let p represent a true statement, while q and r represent false statements. Find the truth value of the compound statement.
-
(True/False)
4.9/5  (37)
(37)
Determine the truth value for each simple statement. Then, using the truth values, give the truth value of the compound statement.
-One dollar has the same value as 5 dimes and one quarter has the same value as 25 pennies, or one dime has the same value as 5 nickels.
(True/False)
5.0/5  (31)
(31)
Translate the statement into symbols then construct a truth table.
- The doctor prescribed medicine.
The patient has recovered.
The doctor did not prescribe medicine but the patient recovered.
(Multiple Choice)
4.8/5  (35)
(35)
Determine which, if any, of the three statements are equivalent.
-I. If the garden needs watering, then the garden needs weeding or the garden is not lovely.
II. The garden needs watering, and it is false that the garden does not need weeding and the Garden is not lovely.
III. The garden needs watering, and the garden needs weeding or the garden is lovely.
(Multiple Choice)
4.8/5  (46)
(46)
Translate the statement into symbols then construct a truth table.
- The garden contains sunflowers.
The fence is painted white.
The lawnmower is electric.
The garden contains sunflowers or the fence is painted white, or the lawnmower is electric.
(Multiple Choice)
4.8/5  (37)
(37)
Write the compound statement in symbols.
Let r = ʺThe food is good,ʺ p = ʺI eat too much,ʺ q = ʺIʹll exercise.ʺ
-If the food is not good, I wonʹt eat too much.
(Multiple Choice)
4.8/5  (40)
(40)
Select letters to represent the simple statements and write each statement symbolically by using parentheses then indicate whether the statement is a negation, conjunction, disjunction, conditional, or biconditional.
-If a number is divisible by 3 and the number is not divisible by 2 then the number is not divisible By 6.
(Multiple Choice)
4.9/5  (41)
(41)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.9/5  (35)
(35)
Use DeMorganʹs laws or a truth table to determine whether the two statements are equivalent.
-
(Multiple Choice)
4.8/5  (33)
(33)
Use the information given in the chart or graph to determine the truth values of the simple statements. Then determine the truth value of the compound statement given.
-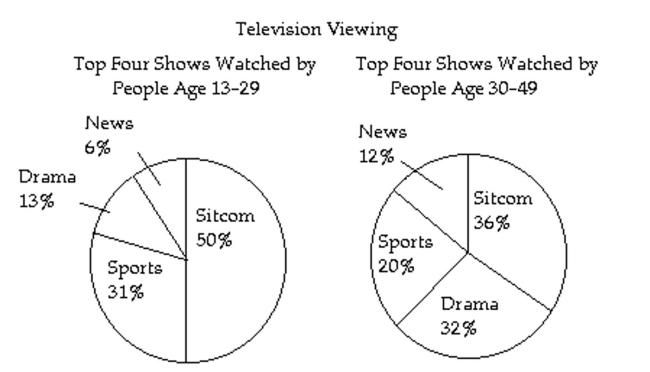 36% of 30-49 year-olds watch sitcoms if and only if 6% of 13-29 year-olds watch news and younger viewers watch sports less often than older viewers.
36% of 30-49 year-olds watch sitcoms if and only if 6% of 13-29 year-olds watch news and younger viewers watch sports less often than older viewers.
(True/False)
4.8/5  (35)
(35)
Write the indicated statement. Use De Morgan's Laws if necessary.
-If , then
Converse
(Multiple Choice)
4.9/5  (31)
(31)
Write the indicated statement. Use De Morgan's Laws if necessary.
-If I pass, Iʹll party.
Contrapositive
(Multiple Choice)
4.8/5  (44)
(44)
Let p represent a true statement, while q and r represent false statements. Find the truth value of the compound statement.
-
(True/False)
4.9/5  (35)
(35)
Showing 141 - 160 of 201
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)