Exam 3: Logic
Exam 1: Critical Thinking Skills95 Questions
Exam 2: Sets126 Questions
Exam 3: Logic201 Questions
Exam 4: Systems of Numeration162 Questions
Exam 5: Number Theory and the Real Number System197 Questions
Exam 7: Algebra, Graphs, and Functions188 Questions
Exam 8: The Metric System188 Questions
Exam 9: Geometry147 Questions
Exam 10: Consumer Mathematics221 Questions
Exam 11: Probability309 Questions
Exam 14: Voting and Apportionment71 Questions
Select questions type
Use DeMorganʹs laws or a truth table to determine whether the two statements are equivalent.
-
(Multiple Choice)
4.9/5  (33)
(33)
Determine whether the statement is a self-contradiction, an implication, a tautology (that is not also an implication), or none of these.
-
(Multiple Choice)
4.7/5  (44)
(44)
Translate the statement into symbols then construct a truth table.
- Parker will work in an office.
= Parker will work as a forest ranger.
Parker will work as a landscape architect.
Parker will not work in an office, but he will work as a forest ranger or a landscape architect.
(Multiple Choice)
4.7/5  (36)
(36)
Indicate whether the statement is a simple or a compound statement. If it is a compound statement, indicate whether it is a negation, conjunction, disjunction, conditional, or biconditional by using both the word and its appropriate symbol.
-The apartment is rented or it is available.
(Multiple Choice)
4.7/5  (34)
(34)
Use DeMorganʹs laws or a truth table to determine whether the two statements are equivalent.
-
(Multiple Choice)
4.9/5  (36)
(36)
Use the information given in the chart or graph to determine the truth values of the simple statements. Then determine the truth value of the compound statement given.
- Planet X \bullet Moon 1 o Moon 2 Diameter of moons: May have: o Moon 3 o 3-8 o water ice \circ Moon 4 \circ9-14 \bullet atmosphere 0 Moon 5 \bullet15-24 o both
Moon 1 has a smaller diameter than Moon 3 and Moon 5 may have water ice, if and only if Moon 2 may have both water ice and an atmosphere.
(True/False)
4.9/5  (36)
(36)
Write an equivalent sentence for the statement.
-If the box is in the mail, then it should be here by tomorrow. (Hint: Use the fact that p → q is Equivalent to ~p ∨ q.)
(Multiple Choice)
4.7/5  (41)
(41)
Use DeMorganʹs laws or a truth table to determine whether the two statements are equivalent.
-
(Multiple Choice)
4.9/5  (27)
(27)
Write the indicated statement. Use De Morgan's Laws if necessary.
-If you like me, then I like you.
Converse
(Multiple Choice)
4.9/5  (37)
(37)
Determine which, if any, of the three statements are equivalent.
-I. Gasoline costs $1.99 per gallon if and only if you live in Cook County.
II. You do not live in Cook County and gasoline does not cost $1.99 per gallon.
III. If you do not live in Cook County then gasoline does not cost $1.99 per gallon and if gasoline Does not cost $1.99 per gallon then you do not live in Cook County.
(Multiple Choice)
4.8/5  (43)
(43)
Write the compound statement in words.
-Let "The puppy is trained."
= "The puppy behaves well." = "His owners are happy." \sim(p\rightarrowq)
(Multiple Choice)
4.9/5  (34)
(34)
Let p represent a true statement, while q and r represent false statements. Find the truth value of the compound statement.
-
(True/False)
4.9/5  (40)
(40)
Write an equivalent sentence for the statement.
-If you canʹt take the heat, stay out of the sun. (Hint: Use the fact that p → q is equivalent to ~p ∨ q.)
(Multiple Choice)
4.9/5  (37)
(37)
Let p represent the statement, ʺJim plays footballʺ, and let q represent ʺMichael plays basketballʺ. Convert the compound statements into symbols.
-Jim plays football and Michael plays basketball.
(Multiple Choice)
4.7/5  (38)
(38)
Write the compound statement in symbols. Then construct a truth table for the symbolic statement.
Let r = ʺThe food is good,ʺ p = ʺI eat too much,ʺ q = ʺIʹll exercise.ʺ
-If I eat too much, then I?ll exercise.
(Multiple Choice)
4.8/5  (40)
(40)
Indicate whether the statement is a simple or a compound statement. If it is a compound statement, indicate whether it is a negation, conjunction, disjunction, conditional, or biconditional by using both the word and its appropriate symbol.
-It is false that whales are fish and bats are birds.
(Multiple Choice)
4.8/5  (31)
(31)
Determine the truth value for the simple statement. Then use these truth values to determine the truth value of the compound statement. Use the chart or graph when provided.
-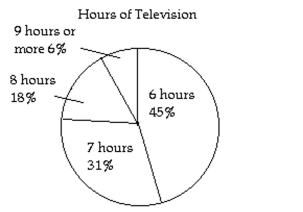 Thirty-one percent of people watch 7 hours of TV each week or 6% do not watch 9 or more hours of TV each week, and 18% watch 8 hours of TV each week.
Thirty-one percent of people watch 7 hours of TV each week or 6% do not watch 9 or more hours of TV each week, and 18% watch 8 hours of TV each week.
(True/False)
4.8/5  (42)
(42)
Determine the truth value for the simple statement. Then use these truth values to determine the truth value of the compound statement. Use the chart or graph when provided.
-9 + 8 = 20 - 3 or 36 ÷ 3 = 2 + 6
(True/False)
4.7/5  (43)
(43)
Showing 161 - 180 of 201
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)