Exam 3: Logic
Exam 1: Critical Thinking Skills95 Questions
Exam 2: Sets126 Questions
Exam 3: Logic201 Questions
Exam 4: Systems of Numeration162 Questions
Exam 5: Number Theory and the Real Number System197 Questions
Exam 7: Algebra, Graphs, and Functions188 Questions
Exam 8: The Metric System188 Questions
Exam 9: Geometry147 Questions
Exam 10: Consumer Mathematics221 Questions
Exam 11: Probability309 Questions
Exam 14: Voting and Apportionment71 Questions
Select questions type
Write the compound statement in symbols.
Let r = ʺThe food is good,ʺ p = ʺI eat too much,ʺ q = ʺIʹll exercise.ʺ
-If the food is good or if I eat too much, Iʹll exercise.
(Multiple Choice)
4.8/5  (32)
(32)
Write an equivalent sentence for the statement.
-You do not give your rain coat to the doorman or he will give you a dirty look. (Hint: Use the fact That p → qis equivalent to ~p ∨ q.)
(Multiple Choice)
4.8/5  (39)
(39)
Indicate whether the statement is a simple or a compound statement. If it is a compound statement, indicate whether it is a negation, conjunction, disjunction, conditional, or biconditional by using both the word and its appropriate symbol.
-The clown is not amusing.
(Multiple Choice)
4.9/5  (33)
(33)
Determine the truth value for each simple statement. Then, using the truth values, give the truth value of the compound statement.
-A foot is equal to 16 inches, if and only if a meter is equal to 100 centimeters and a yard is equal to 5 feet.
(True/False)
4.9/5  (36)
(36)
Write the compound statement in symbols. Then construct a truth table for the symbolic statement.
Let r = ʺThe food is good,ʺ p = ʺI eat too much,ʺ q = ʺIʹll exercise.ʺ
-If the food is not good, I won?t eat too much.
(Multiple Choice)
4.8/5  (37)
(37)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.9/5  (40)
(40)
Write the compound statement in symbols. Then construct a truth table for the symbolic statement.
Let r = ʺThe food is good,ʺ p = ʺI eat too much,ʺ q = ʺIʹll exercise.ʺ
-The food is good and if I eat too much, then I?ll exercise.
(Multiple Choice)
4.9/5  (34)
(34)
Use the information given in the chart or graph to determine the truth values of the simple statements. Then determine the truth value of the compound statement given.
-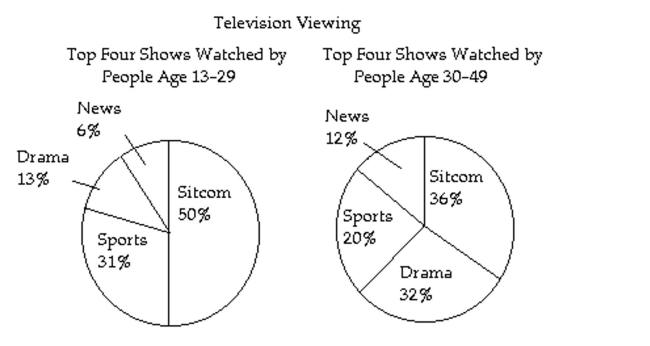 The most common type of TV show watched by 13-29 year-olds is the sitcom, or 31% of 13-29 year-olds watch sports and 20% of 30-49 year-olds watch sports.
The most common type of TV show watched by 13-29 year-olds is the sitcom, or 31% of 13-29 year-olds watch sports and 20% of 30-49 year-olds watch sports.
(True/False)
4.8/5  (25)
(25)
Determine which, if any, of the three statements are equivalent.
-I. The raft flipped if and only if the guide misjudged the rapid or the crew fell overboard.
II. The crew fell overboard, or if the guide misjudged the rapid then the raft flipped.
III. If the guide misjudged the rapid, then the raft flipped or the crew fell overboard.
(Multiple Choice)
4.9/5  (49)
(49)
Write the compound statement in symbols.
Let r = ʺThe food is good,ʺ p = ʺI eat too much,ʺ q = ʺIʹll exercise.ʺ
-Iʹll exercise if I donʹt eat too much.
(Multiple Choice)
4.9/5  (39)
(39)
Convert the compound statement into words.
- "Her name is Lisa."
"She lives in Chicago."
(Multiple Choice)
4.8/5  (42)
(42)
Use DeMorganʹs laws or a truth table to determine whether the two statements are equivalent.
-
(Multiple Choice)
4.8/5  (40)
(40)
Indicate whether the statement is a simple or a compound statement. If it is a compound statement, indicate whether it is a negation, conjunction, disjunction, conditional, or biconditional by using both the word and its appropriate symbol.
-The team leader has decided to take a vacation.
(Multiple Choice)
4.9/5  (32)
(32)
Determine whether the statement is a self-contradiction, an implication, a tautology (that is not also an implication), or none of these.
-
(Multiple Choice)
4.7/5  (32)
(32)
Indicate whether the statement is a simple or a compound statement. If it is a compound statement, indicate whether it is a negation, conjunction, disjunction, conditional, or biconditional by using both the word and its appropriate symbol.
-The animal is a mammal if and only if it nurses its young.
(Multiple Choice)
4.9/5  (43)
(43)
Identify the standard form of the argument.
- \rightarrow \sim \therefore\sim
(Multiple Choice)
4.8/5  (39)
(39)
Write the compound statement in symbols.
Let r = ʺThe food is good,ʺ p = ʺI eat too much,ʺ q = ʺIʹll exercise.ʺ
-If I exercise, then I wonʹt eat too much.
(Multiple Choice)
4.8/5  (34)
(34)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.7/5  (36)
(36)
Showing 181 - 200 of 201
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)