Exam 3: Logic
Exam 1: Critical Thinking Skills95 Questions
Exam 2: Sets126 Questions
Exam 3: Logic201 Questions
Exam 4: Systems of Numeration162 Questions
Exam 5: Number Theory and the Real Number System197 Questions
Exam 7: Algebra, Graphs, and Functions188 Questions
Exam 8: The Metric System188 Questions
Exam 9: Geometry147 Questions
Exam 10: Consumer Mathematics221 Questions
Exam 11: Probability309 Questions
Exam 14: Voting and Apportionment71 Questions
Select questions type
Use truth tables to test the validity of the argument.
- \vee \sim(\vee) \therefore\sim
(Multiple Choice)
4.9/5  (42)
(42)
Let p represent the statement, ʺJim plays footballʺ, and let q represent ʺMichael plays basketballʺ. Convert the compound statements into symbols.
-Jim does not play football and Michael does not play basketball.
(Multiple Choice)
4.8/5  (37)
(37)
Determine the truth value for the simple statement. Then use these truth values to determine the truth value of the compound statement. Use the chart or graph when provided.
-9 + 8 = 20 - 3 and 36 ÷ 3 = 6 + 2
(True/False)
4.7/5  (27)
(27)
Let p represent a true statement, while q and r represent false statements. Find the truth value of the compound statement.
-
(True/False)
4.8/5  (29)
(29)
Determine the truth value for the simple statement. Then use these truth values to determine the truth value of the compound statement. Use the chart or graph when provided.
-0 > -3 or 3 ≥ 10
(True/False)
4.9/5  (42)
(42)
Write the indicated statement. Use De Morgan's Laws if necessary.
-If the chores are done, then we will go to the carnival and we will eat cotton candy.
Contrapositive
(Multiple Choice)
4.9/5  (40)
(40)
Let p represent the statement, ʺJim plays footballʺ, and let q represent ʺMichael plays basketballʺ. Convert the compound statements into symbols.
-Jim does not play football or Michael does not play basketball.
(Multiple Choice)
4.7/5  (30)
(30)
Let p represent a true statement, while q and r represent false statements. Find the truth value of the compound statement.
-
(True/False)
4.9/5  (41)
(41)
Select letters to represent the simple statements and write each statement symbolically by using parentheses then indicate whether the statement is a negation, conjunction, disjunction, conditional, or biconditional.
-If tomorrow is not Saturday then today is Friday if and only if tomorrow is Saturday.
(Multiple Choice)
4.8/5  (31)
(31)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.7/5  (44)
(44)
Determine whether the statement is a self-contradiction, an implication, a tautology (that is not also an implication), or none of these.
-
(Multiple Choice)
4.9/5  (38)
(38)
Given p is true, q is true, and r is false, find the truth value of the statement.
-
(True/False)
4.9/5  (32)
(32)
Use the information given in the chart or graph to determine the truth values of the simple statements. Then determine the truth value of the compound statement given.
-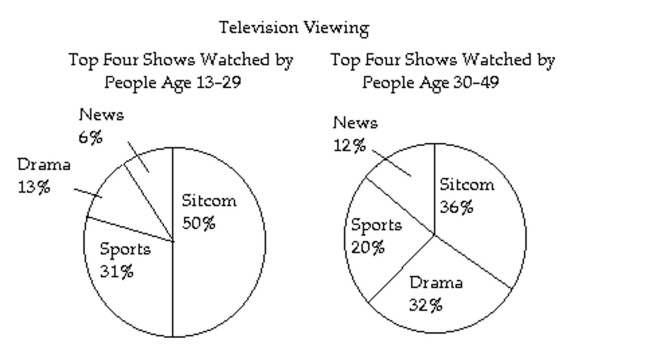 If older viewers watch fewer drama programs than younger viewers and younger viewers watch dramas less than 25% of the time, then older viewers watch drama programs less than 25% of the time.
If older viewers watch fewer drama programs than younger viewers and younger viewers watch dramas less than 25% of the time, then older viewers watch drama programs less than 25% of the time.
(True/False)
4.9/5  (43)
(43)
Determine which, if any, of the three statements are equivalent.
-I. Jan is well or Jan is still recovering.
II. If Jan is still recovering, then Jan is not well.
III. If Jan is well, then Jan is not still recovering.
(Multiple Choice)
4.7/5  (30)
(30)
Determine the truth value for the simple statement. Then use these truth values to determine the truth value of the compound statement. Use the chart or graph when provided.
-0 > -7 or 4 ≥ 10, and -4 ≤ 7
(True/False)
4.7/5  (40)
(40)
Showing 21 - 40 of 201
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)