Question 1

Find the area of triangle ABC with the given parts. Round to the nearest tenth when necessary.
-$$\begin{array} { l } 
\mathrm { b } = 9.1 \mathrm { ft } \
\mathrm { A } = 35 ^ { \circ } 20 ^ { \prime } \
\mathrm { C } = 106 ^ { \circ } 20 ^ { \prime }
\end{array}$$

Accepted Answer

A)  $37 \mathrm { ft } ^ { 2 }$ 
B)  $79 \mathrm { ft } ^ { 2 }$ 
C)  $32 \mathrm { ft } ^ { 2 }$ 
D)  $74 \mathrm { ft } ^ { 2 }$ 
A)  $37 \mathrm { ft } ^ { 2 }$ 
B)  $79 \mathrm { ft } ^ { 2 }$ 
C)  $32 \mathrm { ft } ^ { 2 }$ 
D)  $74 \mathrm { ft } ^ { 2 }$

Question 2

Find the missing parts of the triangle.
-$$\begin{array} { l } 
\mathrm { A } = 23 ^ { \circ } \
\mathrm { a } = 35 \mathrm {~km} \
\mathrm {~b} = 54 \mathrm {~km}
\end{array}$$
If necessary, round angles to the nearest whole number and side lengths to the nearest $\mathrm { km }$.

Accepted Answer

A)  $\mathrm { B } _ { 1 } = 37 ^ { \circ } , \mathrm { C } _ { 1 } = 120 ^ { \circ } , \mathrm { c } 1 = 78 \mathrm {~km}$ 
B)  $\mathrm { B } = 37 ^ { \circ } , \mathrm { C } = 120 ^ { \circ } , \mathrm { c } = 78 \mathrm {~km}$
$$\mathrm { B } _ { 2 } = 143 ^ { \circ } , \mathrm { C } _ { 2 } = 14 ^ { \circ } , \mathrm { c } _ { 2 } = 22 \mathrm {~km}$$ 
C)  no such triangle
$$\text { 
D)  } \begin{aligned}
\mathrm { B } _ { 1 } & = 120 ^ { \circ } , \mathrm { C } _ { 1 } = 37 ^ { \circ } , \mathrm { c } _ { 1 } = 78 \mathrm {~km} \
\mathrm {~B} _ { 2 } & = 14 ^ { \circ } , \mathrm { C } _ { 2 } = 143 ^ { \circ } , \mathrm { c } _ { 2 } = 22 \mathrm {~km}
\end{aligned}$$ 
A)  $\mathrm { B } _ { 1 } = 37 ^ { \circ } , \mathrm { C } _ { 1 } = 120 ^ { \circ } , \mathrm { c } 1 = 78 \mathrm {~km}$ 
B)  $\mathrm { B } = 37 ^ { \circ } , \mathrm { C } = 120 ^ { \circ } , \mathrm { c } = 78 \mathrm {~km}$
$$\mathrm { B } _ { 2 } = 143 ^ { \circ } , \mathrm { C } _ { 2 } = 14 ^ { \circ } , \mathrm { c } _ { 2 } = 22 \mathrm {~km}$$ 
C)  no such triangle
$$\text { 
D)  } \begin{aligned}
\mathrm { B } _ { 1 } & = 120 ^ { \circ } , \mathrm { C } _ { 1 } = 37 ^ { \circ } , \mathrm { c } _ { 1 } = 78 \mathrm {~km} \
\mathrm {~B} _ { 2 } & = 14 ^ { \circ } , \mathrm { C } _ { 2 } = 143 ^ { \circ } , \mathrm { c } _ { 2 } = 22 \mathrm {~km}
\end{aligned}$$

Question 3

Given that the polar equation r models the orbits of the planets about the sun,
-Suppose that a radio signal transmission pattern can be modeled by $r = 32 + 32 \sin \theta$, for $0 ^ { \circ } \leq \theta \leq 360 ^ { \circ }$, where the units are miles. Assume that the positive $x$-axis points east, and determine the distances of transmission in the east, north, west, and south directions.

Accepted Answer

A)  E: 32 miles, N: 32 miles, W: 32 miles, S: 0 miles 
B)  E: 64 miles, N: 32 miles, W: 0 miles, S: 32 miles 
C)  E: 32 miles, N: 64 miles, W: 32 miles, S: 0 miles 
D)  E: 32 miles, N: 0 miles, $W : 32$ miles, S: 64 miles 
A)  E: 32 miles, N: 32 miles, W: 32 miles, S: 0 miles 
B)  E: 64 miles, N: 32 miles, W: 0 miles, S: 32 miles 
C)  E: 32 miles, N: 64 miles, W: 32 miles, S: 0 miles 
D)  E: 32 miles, N: 0 miles, $W : 32$ miles, S: 64 miles

Question 4

Solve the problem.
-If u =-5, 7 , v =3, 6, and w =-11, 2 , evaluate u ·v + u ·w.

Accepted Answer

A)  104 
B)  96 
C)  86 
D)  77 
A)  104 
B)  96 
C)  86 
D)  77

Question 5

For the given rectangular equation, give its equivalent polar equation.
-$$x ^ { 2 } + y ^ { 2 } = 36$$

Accepted Answer

A)  $r = 6 \sin \theta$ 
B)  $r = 36$ 
C)  $r = 6 \cos \theta$ 
D)  $r = 6$ 
A)  $r = 6 \sin \theta$ 
B)  $r = 36$ 
C)  $r = 6 \cos \theta$ 
D)  $r = 6$

Question 6

Give two parametric representations for the equation of the parabola.
-$$y = ( x - 2 ) ^ { 2 } - 1$$

Accepted Answer

A)  $x = t , y = ( t + 2 ) ^ { 2 } - 1$ for $t$ in $( \infty , \infty ) ; x = t + 2 , y = t ^ { 2 } - 1$ for $t$ in $( \infty , \infty )$ 
B)  $x = t , y = ( t - 2 ) ^ { 2 } - 1$ for $t$ in $( \infty , \infty ) ; x = t + 2 , y = t ^ { 2 } - 1$ for $t$ in $( \infty , \infty )$ 
C)  $x = t , y = ( t - 2 ) ^ { 2 } - 1$ for $t$ in $( \infty , \infty ) ; x = t - 2 , y = t ^ { 2 } - 1$ for $t$ in $( \infty , \infty )$ 
D)  $x = t , y = ( t + 2 ) ^ { 2 } - 1$ for $t$ in $( \infty , \infty )$; $x = t - 2 , y = t ^ { 2 } - 1$ for $t$ in $( \infty , \infty )$ 
A)  $x = t , y = ( t + 2 ) ^ { 2 } - 1$ for $t$ in $( \infty , \infty ) ; x = t + 2 , y = t ^ { 2 } - 1$ for $t$ in $( \infty , \infty )$ 
B)  $x = t , y = ( t - 2 ) ^ { 2 } - 1$ for $t$ in $( \infty , \infty ) ; x = t + 2 , y = t ^ { 2 } - 1$ for $t$ in $( \infty , \infty )$ 
C)  $x = t , y = ( t - 2 ) ^ { 2 } - 1$ for $t$ in $( \infty , \infty ) ; x = t - 2 , y = t ^ { 2 } - 1$ for $t$ in $( \infty , \infty )$ 
D)  $x = t , y = ( t + 2 ) ^ { 2 } - 1$ for $t$ in $( \infty , \infty )$; $x = t - 2 , y = t ^ { 2 } - 1$ for $t$ in $( \infty , \infty )$

Question 7

Use the parallelogram rule to find the magnitude of the resultant force for the two forces shown in the figure. Round to
one decimal place.
-Two boats are pulling a disabled vessel toward the landing dock with forces of $940 \mathrm { lb }$ and $930 \mathrm { lb }$. The angle between the forces is $25.7 ^ { \circ }$. Find the direction and magnitude of the equilibrant.

Accepted Answer

A)  $182 \mathrm { lb }$ at an angle of $167.2 ^ { \circ }$ with the $940 - \mathrm { lb }$ force 
B)  $1823 \mathrm { lb }$ at an angle of $12.8 ^ { \circ }$ with the $940 - \mathrm { lb }$ force 
C)  $1823 \mathrm { lb }$ at an angle of $77.2 ^ { \circ }$ with the $930 - \mathrm { lb }$ force 
D)  $1823 \mathrm { lb }$ at an angle of $167.2 ^ { \circ }$ with the $940 - \mathrm { lb }$ force 
A)  $182 \mathrm { lb }$ at an angle of $167.2 ^ { \circ }$ with the $940 - \mathrm { lb }$ force 
B)  $1823 \mathrm { lb }$ at an angle of $12.8 ^ { \circ }$ with the $940 - \mathrm { lb }$ force 
C)  $1823 \mathrm { lb }$ at an angle of $77.2 ^ { \circ }$ with the $930 - \mathrm { lb }$ force 
D)  $1823 \mathrm { lb }$ at an angle of $167.2 ^ { \circ }$ with the $940 - \mathrm { lb }$ force

Question 8

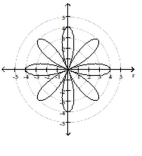
The graph of a polar equation is given. Select the polar equation for the graph.
-

Accepted Answer

A)  $r = 4 + \cos ( 4 \theta )$ 
B)  $r = 4$ 
C)  $r = 4 \sin ( 4 \theta )$ 
D)  $r = 4 \cos ( 4 \theta$ 
A)  $r = 4 + \cos ( 4 \theta )$ 
B)  $r = 4$ 
C)  $r = 4 \sin ( 4 \theta )$ 
D)  $r = 4 \cos ( 4 \theta$

Question 9

Solve the problem.
-A projectile is fired with an initial velocity of 350 feet per second at an angle of 70° with the horizontal. To the nearest foot, find the maximum altitude of the projectile.

Accepted Answer

A)  1706 ft 
B)  1690 ft 
C)  1682 ft 
D)  1673 ft 
A)  1706 ft 
B)  1690 ft 
C)  1682 ft 
D)  1673 ft

Question 10

Give two parametric representations for the equation of the parabola.
-$$y = x ^ { 2 } + 6 x + 15$$

Accepted Answer

A)  $x = t , y = t ^ { 2 } + 6 t + 15$ for $t$ in $( \infty , \infty ) ; x = t - 3 , y = t ^ { 2 } + 6$ for $t$ in $( \infty , \infty )$ 
B)  $x = t , y = t ^ { 2 } - 6 t - 15$ for $t$ in $( \infty , \infty ) ; x = t + 3 , y = t ^ { 2 } + 6$ for $t$ in $( \infty , \infty )$ 
C)  $x = t , y = t ^ { 2 } + 6 t + 15$ for $t$ in $( \infty , \infty ) ; x = t + 3 , y = t ^ { 2 } + 6$ for $t$ in $( \infty , \infty )$ 
D)  $x = t , y = t ^ { 2 } + 6 t + 15$ for $t$ in $( \infty , \infty ) ; x = t - 3 , y = t ^ { 2 } - 6$ for $t$ in $( \infty , \infty )$ 
A)  $x = t , y = t ^ { 2 } + 6 t + 15$ for $t$ in $( \infty , \infty ) ; x = t - 3 , y = t ^ { 2 } + 6$ for $t$ in $( \infty , \infty )$ 
B)  $x = t , y = t ^ { 2 } - 6 t - 15$ for $t$ in $( \infty , \infty ) ; x = t + 3 , y = t ^ { 2 } + 6$ for $t$ in $( \infty , \infty )$ 
C)  $x = t , y = t ^ { 2 } + 6 t + 15$ for $t$ in $( \infty , \infty ) ; x = t + 3 , y = t ^ { 2 } + 6$ for $t$ in $( \infty , \infty )$ 
D)  $x = t , y = t ^ { 2 } + 6 t + 15$ for $t$ in $( \infty , \infty ) ; x = t - 3 , y = t ^ { 2 } - 6$ for $t$ in $( \infty , \infty )$

Question 11

The graph o $$r = a \theta$$ in polar coordinates is an example of the spiral of Archimedes. With your calculator set to radian
mode, use the given value of a and interval of  to graph the spiral in the window specified.
-$a = - 0.5 , - \pi \leq \theta \leq 4 \pi , [ - 6,6 ]$ by $[ - 6,6 ]$

Accepted Answer

A) 
  
B) 
  
C) 
  
D) 
  
A) 
  
B) 
  
C) 
  
D)

Question 12

The rectangular coordinates of a point are given. Express the point in polar coordinates with $$r \geq 0 \text { and } 0 ^ { \circ } \leq \theta < 360 ^ { \circ } \text {. }$$
-$$( 0 , - 4 )$$

Accepted Answer

A)  $\left( 4,270 ^ { \circ } \right)$ 
B)  $\left( 4,180 ^ { \circ } \right)$ 
C)  $\left( 4,0 ^ { \circ } \right)$ 
D)  $\left( 4,90 ^ { \circ } \right)$ 
A)  $\left( 4,270 ^ { \circ } \right)$ 
B)  $\left( 4,180 ^ { \circ } \right)$ 
C)  $\left( 4,0 ^ { \circ } \right)$ 
D)  $\left( 4,90 ^ { \circ } \right)$

Question 13

Answer the question.
-In which quadrants do the nonreal cube roots of $- 1$ lie?

Accepted Answer

A)  The second and fourth quadrants 
B)  The second and third quadrants 
C)  The first and fourth quadrants 
D)  The first and third quadrants 
A)  The second and fourth quadrants 
B)  The second and third quadrants 
C)  The first and fourth quadrants 
D)  The first and third quadrants

Question 14

Find all specified roots.
-Eighth roots of $i$.

Accepted Answer

A)  $\frac { 1 } { \sqrt { 2 } } + \frac { 1 } { \sqrt { 2 } } \mathrm { i } , \frac { 1 } { \sqrt { 2 } } - \frac { 1 } { \sqrt { 2 } } \mathrm { i } , - \frac { 1 } { \sqrt { 2 } } + \frac { 1 } { \sqrt { 2 } } \mathrm { i } , - \frac { 1 } { \sqrt { 2 } } - \frac { 1 } { \sqrt { 2 } } \mathrm { i }$ 
B)  $1 , - 1 , i , - i$ 
C)  $\operatorname { cis } \frac { \pi } { 16 } , \operatorname { cis } \frac { 5 \pi } { 16 } , \operatorname { cis } \frac { 9 \pi } { 16 } , \operatorname { cis } \frac { 13 \pi } { 16 } , \operatorname { cis } \frac { 17 \pi } { 16 }$, cis $\frac { 21 \pi } { 16 } , \operatorname { cis } \frac { 25 \pi } { 16 } , \operatorname { cis } \frac { 29 \pi } { 16 }$ 
D)  $1 , - 1 , i , - i , \frac { 1 } { \sqrt { 2 } } + \frac { 1 } { \sqrt { 2 } } i , \frac { 1 } { \sqrt { 2 } } - \frac { 1 } { \sqrt { 2 } } \mathrm { i } , - \frac { 1 } { \sqrt { 2 } } + \frac { 1 } { \sqrt { 2 } } \mathrm { i } , - \frac { 1 } { \sqrt { 2 } } - \frac { 1 } { \sqrt { 2 } } \mathrm { i }$ 
A)  $\frac { 1 } { \sqrt { 2 } } + \frac { 1 } { \sqrt { 2 } } \mathrm { i } , \frac { 1 } { \sqrt { 2 } } - \frac { 1 } { \sqrt { 2 } } \mathrm { i } , - \frac { 1 } { \sqrt { 2 } } + \frac { 1 } { \sqrt { 2 } } \mathrm { i } , - \frac { 1 } { \sqrt { 2 } } - \frac { 1 } { \sqrt { 2 } } \mathrm { i }$ 
B)  $1 , - 1 , i , - i$ 
C)  $\operatorname { cis } \frac { \pi } { 16 } , \operatorname { cis } \frac { 5 \pi } { 16 } , \operatorname { cis } \frac { 9 \pi } { 16 } , \operatorname { cis } \frac { 13 \pi } { 16 } , \operatorname { cis } \frac { 17 \pi } { 16 }$, cis $\frac { 21 \pi } { 16 } , \operatorname { cis } \frac { 25 \pi } { 16 } , \operatorname { cis } \frac { 29 \pi } { 16 }$ 
D)  $1 , - 1 , i , - i , \frac { 1 } { \sqrt { 2 } } + \frac { 1 } { \sqrt { 2 } } i , \frac { 1 } { \sqrt { 2 } } - \frac { 1 } { \sqrt { 2 } } \mathrm { i } , - \frac { 1 } { \sqrt { 2 } } + \frac { 1 } { \sqrt { 2 } } \mathrm { i } , - \frac { 1 } { \sqrt { 2 } } - \frac { 1 } { \sqrt { 2 } } \mathrm { i }$

Question 15

Provide an appropriate response.
-Which of the following pairs of parametric equations will graph a semicircle?

Accepted Answer

A)  $x = \cos \frac { 1 } { 2 } t , y = \sin \frac { 1 } { 2 } t , 0 \leq t \leq \pi$ 
B)  $x = \cos 2 t , y = \sin 2 t , 0 \leq t \leq \pi$ 
C)  $x = \cos \frac { 1 } { 4 } t , y = \sin \frac { 1 } { 4 } t , 0 \leq t \leq 4 \pi$ 
D)  $x = \cos t , y = \sin t , 0 \leq t \leq \frac { \pi } { 2 }$ 
A)  $x = \cos \frac { 1 } { 2 } t , y = \sin \frac { 1 } { 2 } t , 0 \leq t \leq \pi$ 
B)  $x = \cos 2 t , y = \sin 2 t , 0 \leq t \leq \pi$ 
C)  $x = \cos \frac { 1 } { 4 } t , y = \sin \frac { 1 } { 4 } t , 0 \leq t \leq 4 \pi$ 
D)  $x = \cos t , y = \sin t , 0 \leq t \leq \frac { \pi } { 2 }$

Question 16

Find the product. Write the product in rectangular form, using exact values.
-$\left[ 4 \operatorname { cis } 45 ^ { \circ } \right] \left[ 6 \operatorname { cis } 225 ^ { \circ } \right]$

Accepted Answer

A)  $24 \mathrm { i }$ 
B)  24 
C)  $- 24 \mathrm { i }$ 
D)  $- 24$ 
A)  $24 \mathrm { i }$ 
B)  24 
C)  $- 24 \mathrm { i }$ 
D)  $- 24$

Question 17

Give the rectangular coordinates for the point.
-$( - 2 , \pi )$

Accepted Answer

A)  $( 0,2 )$ 
B)  $( 2,0 )$ 
C)  $( - 2,0 )$ 
D)  $( 0 , - 2 )$ 
A)  $( 0,2 )$ 
B)  $( 2,0 )$ 
C)  $( - 2,0 )$ 
D)  $( 0 , - 2 )$

Question 18

Find the indicated vector.
-Let $\mathbf { u } = \langle 6,2 \rangle , \mathbf { v } = \langle - 8,6 \rangle$. Find $\mathbf { v } - \mathbf { u }$.

Accepted Answer

A)  $\langle - 2,8 \rangle$ 
B)  $\langle - 14,4 \rangle$ 
C)  $\langle - 4,14 \rangle$ 
D)  $\langle 0 , - 10 \rangle$ 
A)  $\langle - 2,8 \rangle$ 
B)  $\langle - 14,4 \rangle$ 
C)  $\langle - 4,14 \rangle$ 
D)  $\langle 0 , - 10 \rangle$

Question 19

Find the area of triangle ABC with the given parts. Round to the nearest tenth when necessary.
-Two airplanes leave an airport at the same time, one going northwest (bearing $135 ^ { \circ }$ ) at $410 \mathrm { mph }$ and the other going east at $333 \mathrm { mph }$. How far apart are the planes after 4 hours (to the nearest mile)?

Accepted Answer

A)  $2158 \mathrm { mi }$ 
B)  $2288 \mathrm { mi }$ 
C)  $687 \mathrm { mi }$ 
D)  $2748 \mathrm { mi }$ 
A)  $2158 \mathrm { mi }$ 
B)  $2288 \mathrm { mi }$ 
C)  $687 \mathrm { mi }$ 
D)  $2748 \mathrm { mi }$

Question 20

Use the figure to find the specified vector.
-Find $\mathbf { - a }$.

Accepted Answer

A)  $\langle 7 , - 3 \rangle$ 
B)  $\langle - 7 , - 3 \rangle$ 
C)  $\langle - 3,7 \rangle$ 
D)  $\langle - 3 , - 7 \rangle$ 
A)  $\langle 7 , - 3 \rangle$ 
B)  $\langle - 7 , - 3 \rangle$ 
C)  $\langle - 3,7 \rangle$ 
D)  $\langle - 3 , - 7 \rangle$

Find the area of triangle ABC with the given parts. Round to the nearest tenth when necessary. - =9.1 =32 =102

Find the missing parts of the triangle. - =2 =35 =54 If necessary, round angles to the nearest whole number and side lengths to the nearest $\mathrm { km }$ .

Solve the problem. -If u =-5, 7 , v =3, 6, and w =-11, 2 , evaluate u ·v + u ·w.

For the given rectangular equation, give its equivalent polar equation. - $x ^ { 2 } + y ^ { 2 } = 36$

Give two parametric representations for the equation of the parabola. - $y = ( x - 2 ) ^ { 2 } - 1$

The graph of a polar equation is given. Select the polar equation for the graph. -

Solve the problem. -A projectile is fired with an initial velocity of 350 feet per second at an angle of 70° with the horizontal. To the nearest foot, find the maximum altitude of the projectile.

Give two parametric representations for the equation of the parabola. - $y = x ^ { 2 } + 6 x + 15$

The graph o $r = a \theta$ in polar coordinates is an example of the spiral of Archimedes. With your calculator set to radian mode, use the given value of a and interval of  to graph the spiral in the window specified. - $a = - 0.5 , - \pi \leq \theta \leq 4 \pi , [ - 6,6 ]$ by $[ - 6,6 ]$

The rectangular coordinates of a point are given. Express the point in polar coordinates with $r \geq 0 \text { and } 0 ^ { \circ } \leq \theta < 360 ^ { \circ } \text {. }$ - $( 0 , - 4 )$

Answer the question. -In which quadrants do the nonreal cube roots of $- 1$ lie?

Find all specified roots. -Eighth roots of $i$ .

Provide an appropriate response. -Which of the following pairs of parametric equations will graph a semicircle?

Find the product. Write the product in rectangular form, using exact values. - $\left[ 4 \operatorname { cis } 45 ^ { \circ } \right] \left[ 6 \operatorname { cis } 225 ^ { \circ } \right]$

Give the rectangular coordinates for the point. - $( - 2 , \pi )$

Find the indicated vector. -Let $\mathbf { u } = \langle 6,2 \rangle , \mathbf { v } = \langle - 8,6 \rangle$ . Find $\mathbf { v } - \mathbf { u }$ .

Use the figure to find the specified vector. -Find $\mathbf { - a }$ . $Use the figure to find the specified vector. -Find \mathbf { - a } .$

Review of Basic Concepts

Equations and Inequalities

Graphs and Functions

Polynomial and Rational Functions

Inverse, Exponential, and Logarithmic Functions

Trigonometric Functions

The Circular Functions and Their Graphs

Trigonometric Identities and Equations

Systems and Matrices

Analytic Geometry

Further Topics in Algebra

Filters

Exam 9: Applications of Trigonometry