Exam 9: Applications of Trigonometry
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Find the missing parts of the triangle.
- =118. a=1263 b=1363
If necessary, round angles to the nearest tenth and side lengths to the nearest .
(Multiple Choice)
4.9/5  (45)
(45)
Find the dot product for the pair of vectors.
--15, 10, 0, 8
(Multiple Choice)
4.9/5  (46)
(46)
The rectangular coordinates of a point are given. Express the point in polar coordinates with
-
(Multiple Choice)
4.7/5  (39)
(39)
Assume a triangle ABC has standard labeling. Determine whether SAA, ASA, SSA, SAS, or SSS is given. Then decide
whether the law of sines or the law of cosines should be used to begin solving the triangle.
-a, c, and B
(Multiple Choice)
4.7/5  (30)
(30)
Use a table of values to graph the plane curve defined by the following parametric equations. Find a rectangular equation
for the curve.
-
![Use a table of values to graph the plane curve defined by the following parametric equations. Find a rectangular equation for the curve. - x=3 t, y=t+1, \text { for } t \text { in }[-2,3]](https://storage.examlex.com/TB7514/11ed7c59_0e56_1735_8ff5_d3d0018ab5b4_TB7514_11.jpg)
(Multiple Choice)
4.8/5  (30)
(30)
Determine the number of triangles ABC possible with the given parts.
-
(Multiple Choice)
4.9/5  (35)
(35)
Find the missing parts of the triangle.
- =106. =298 =1353
If necessary, round angles the nearest tenth and side lengths to the nearest .
(Multiple Choice)
4.9/5  (42)
(42)
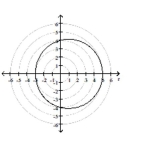
The graph of a polar equation is given. Select the polar equation for the graph.
-
(Multiple Choice)
4.8/5  (32)
(32)
Two forces act at a point in the plane. The angle between the two forces is given. Find the magnitude of the resultant
force.
-forces of 40 and 86 newtons, forming an angle of (round to the nearest newton)
(Multiple Choice)
4.8/5  (44)
(44)
Find all solutions of the equation. Leave answers in trigonometric form.
-
(Multiple Choice)
4.9/5  (36)
(36)
Determine whether the pair of vectors is orthogonal.
-3i - 6j, -6i + 3j
(Multiple Choice)
4.8/5  (33)
(33)
Use the parallelogram rule to find the magnitude of the resultant force for the two forces shown in the figure. Round to
one decimal place.
-A ship leaves point and travels directly north to point . From point , the ship then travels due east to point . The magnitude of the vector from point to point is 128 . Find the magnitude of the northern vector. Find the magnitude of the eastern vector.
(Multiple Choice)
4.7/5  (35)
(35)
Determine the number of triangles ABC possible with the given parts.
-
(Multiple Choice)
4.8/5  (37)
(37)
Two forces act at a point in the plane. The angle between the two forces is given. Find the magnitude of the resultant
force.
-forces of and , forming an angle of (round to the nearest pound)
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-A projectile is fired with an initial velocity of 450 feet per second at an angle of 70° with the horizontal. In how many seconds will the projectile reach its maximum altitude? (Round your
Answer to the nearest tenth of a second.)
(Multiple Choice)
4.9/5  (37)
(37)
Showing 341 - 360 of 447
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)