Question 1

Find the missing parts of the triangle. Round to the nearest tenth when necessary or to the nearest minute as appropriate.
-$$\begin{array} { l } 
a = 7.2 \mathrm { in } . \
\mathrm { b } = 13.7 \mathrm { in } . \
\mathrm { c } = 15.6 \mathrm { in } .
\end{array}$$

Accepted Answer

A)  $\mathrm { A } = 29.5 ^ { \circ } , \mathrm { B } = 59.4 ^ { \circ } , \mathrm { C } = 91.1 ^ { \circ }$ 
B)  No triangle satisfies the given conditions. 
C)  $\mathrm { A } = 25.5 ^ { \circ } , \mathrm { B } = 61.4 ^ { \circ } , \mathrm { C } = 93.1 ^ { \circ }$ 
D)  $\mathrm { A } = 27.5 ^ { \circ } , \mathrm { B } = 61.4 ^ { \circ } , \mathrm { C } = 91.1 ^ { \circ }$ 
A)  $\mathrm { A } = 29.5 ^ { \circ } , \mathrm { B } = 59.4 ^ { \circ } , \mathrm { C } = 91.1 ^ { \circ }$ 
B)  No triangle satisfies the given conditions. 
C)  $\mathrm { A } = 25.5 ^ { \circ } , \mathrm { B } = 61.4 ^ { \circ } , \mathrm { C } = 93.1 ^ { \circ }$ 
D)  $\mathrm { A } = 27.5 ^ { \circ } , \mathrm { B } = 61.4 ^ { \circ } , \mathrm { C } = 91.1 ^ { \circ }$

Question 2

Find a rectangular equation for the plane curve defined by the parametric equations.
-$x = \sqrt { t } , y = 2 t + 5$

Accepted Answer

A)  $y = 2 x ^ { 2 } + 5$ 
B)  $y = 2 \sqrt { x } - 5 , x \geq 0$ 
C)  $y = 2 x ^ { 2 } - 5$ 
D)  $y = 2 \sqrt { x } + 5 , x \geq 0$ 
A)  $y = 2 x ^ { 2 } + 5$ 
B)  $y = 2 \sqrt { x } - 5 , x \geq 0$ 
C)  $y = 2 x ^ { 2 } - 5$ 
D)  $y = 2 \sqrt { x } + 5 , x \geq 0$

Question 3

Find the missing parts of the triangle.
-$$\begin{array} { l } 
\mathrm { A } = 96.1 ^ { \circ } \
\mathrm { b } = 15.2 \mathrm { ft } \
\mathrm { a } = 30.4 \mathrm { ft }
\end{array}$$
If necessary, round angles and side lengths to the nearest tenth.

Accepted Answer

A)  no such triangle 
B)  $\mathrm { B } = 29.8 ^ { \circ } , \mathrm { C } = 54.1 ^ { \circ } , \mathrm { c } = 24.8 \mathrm { ft }$ 
C)  $\mathrm { B } = 34.8 ^ { \circ } , \mathrm { C } = 49.1 ^ { \circ } , \mathrm { c } = 24.8 \mathrm { ft }$ 
D)  $\mathrm { B } = 54.1 ^ { \circ } , \mathrm { C } = 29.8 ^ { \circ } , \mathrm { c } = 24.8 \mathrm { ft }$ 
A)  no such triangle 
B)  $\mathrm { B } = 29.8 ^ { \circ } , \mathrm { C } = 54.1 ^ { \circ } , \mathrm { c } = 24.8 \mathrm { ft }$ 
C)  $\mathrm { B } = 34.8 ^ { \circ } , \mathrm { C } = 49.1 ^ { \circ } , \mathrm { c } = 24.8 \mathrm { ft }$ 
D)  $\mathrm { B } = 54.1 ^ { \circ } , \mathrm { C } = 29.8 ^ { \circ } , \mathrm { c } = 24.8 \mathrm { ft }$

Question 4

Find the missing parts of the triangle. Round to the nearest tenth when necessary or to the nearest minute as appropriate.
-$$\begin{array} { l } 
\mathrm { C } = 105.8 ^ { \circ } \
\mathrm { a } = 4.7 \mathrm {~km} \
\mathrm {~b} = 8.3 \mathrm {~km}
\end{array}$$

Accepted Answer

A)  No triangle satisfies the given conditions. 
B)  $\mathrm { c } = 16.4 \mathrm {~km} , \mathrm {~A} = 23.2 ^ { \circ } , \mathrm { B } = 51 ^ { \circ }$ 
C)  $\mathrm { c } = 10.6 \mathrm {~km} , \mathrm {~A} = 25.2 ^ { \circ } , \mathrm { B } = 49 ^ { \circ }$ 
D)  $\mathrm { c } = 13.5 \mathrm {~km} , \mathrm {~A} = 27.2 ^ { \circ } , \mathrm { B } = 47 ^ { \circ }$ 
A)  No triangle satisfies the given conditions. 
B)  $\mathrm { c } = 16.4 \mathrm {~km} , \mathrm {~A} = 23.2 ^ { \circ } , \mathrm { B } = 51 ^ { \circ }$ 
C)  $\mathrm { c } = 10.6 \mathrm {~km} , \mathrm {~A} = 25.2 ^ { \circ } , \mathrm { B } = 49 ^ { \circ }$ 
D)  $\mathrm { c } = 13.5 \mathrm {~km} , \mathrm {~A} = 27.2 ^ { \circ } , \mathrm { B } = 47 ^ { \circ }$

Question 5

Determine whether the pair of vectors is orthogonal.
-$$\langle - 10 , \sqrt { 3 } \rangle , \langle - 2 \sqrt { 3 } , - 30 \rangle$$

Accepted Answer

A)  Yes 
B)  No 
A)  Yes 
B)  No

Question 6

Find the missing parts of the triangle.
-$$\begin{array} { l } 
A = 44.29 ^ { \circ } \
a = 51.82 \mathrm { yd } \
b = 63.64 \mathrm { yd }
\end{array}$$
If necessary, round angles and side lengths to the nearest hundredth.

Accepted Answer

A)  no such triangle 
B)  $\mathrm { B } _ { 1 } = 76.67 ^ { \circ } , \mathrm { C } _ { 1 } = 59.04 ^ { \circ } , \mathrm { c } _ { 1 } = 72.21 \mathrm { yd }$ $\mathrm { B } _ { 2 } = 14.75 ^ { \circ } , \mathrm { C } _ { 2 } = 120.96 ^ { \circ } , \mathrm { c } _ { 2 } = 18.89 \mathrm { yd }$ 
C)  $\mathrm { B } _ { 1 } = 59.04 ^ { \circ } , \mathrm { C } _ { 1 } = 76.67 ^ { \circ } , \mathrm { c } _ { 1 } = 72.21 \mathrm { yd }$ 
D)  $\mathrm { B } = 59.04 ^ { \circ } , \mathrm { C } = 76.67 ^ { \circ } , \mathrm { c } = 72.21 \mathrm { yd }$ $\mathrm { B } _ { 2 } = 120.96 ^ { \circ } , \mathrm { C } _ { 2 } = 14.75 ^ { \circ } , \mathrm { c } _ { 2 } = 18.89 \mathrm { yd }$ 
A)  no such triangle 
B)  $\mathrm { B } _ { 1 } = 76.67 ^ { \circ } , \mathrm { C } _ { 1 } = 59.04 ^ { \circ } , \mathrm { c } _ { 1 } = 72.21 \mathrm { yd }$ $\mathrm { B } _ { 2 } = 14.75 ^ { \circ } , \mathrm { C } _ { 2 } = 120.96 ^ { \circ } , \mathrm { c } _ { 2 } = 18.89 \mathrm { yd }$ 
C)  $\mathrm { B } _ { 1 } = 59.04 ^ { \circ } , \mathrm { C } _ { 1 } = 76.67 ^ { \circ } , \mathrm { c } _ { 1 } = 72.21 \mathrm { yd }$ 
D)  $\mathrm { B } = 59.04 ^ { \circ } , \mathrm { C } = 76.67 ^ { \circ } , \mathrm { c } = 72.21 \mathrm { yd }$ $\mathrm { B } _ { 2 } = 120.96 ^ { \circ } , \mathrm { C } _ { 2 } = 14.75 ^ { \circ } , \mathrm { c } _ { 2 } = 18.89 \mathrm { yd }$

Question 7

Find the given power. Write answer in rectangular form.
-$$[ - 4 + 4 i \sqrt { 3 } ] ^ { 3 }$$

Accepted Answer

A)  64 
B)  $- 4 + 4 i \sqrt { 3 }$ 
C)  512 
D)  $64 + 12 \mathrm { i } \sqrt { 3 }$ 
A)  64 
B)  $- 4 + 4 i \sqrt { 3 }$ 
C)  512 
D)  $64 + 12 \mathrm { i } \sqrt { 3 }$

Question 8

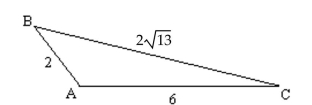
Find the indicated angle or side. Give an exact answer.
-Find the measure of angle A in degrees.

Accepted Answer

A)  $135 ^ { \circ }$ 
B)  $140 ^ { \circ }$ 
C)  $60 ^ { \circ }$ 
D)  $120 ^ { \circ }$ 
A)  $135 ^ { \circ }$ 
B)  $140 ^ { \circ }$ 
C)  $60 ^ { \circ }$ 
D)  $120 ^ { \circ }$

Question 9

Find the area of triangle ABC with the given parts. Round to the nearest tenth when necessary.
-Two points A and B are on opposite sides of a building. A surveyor chooses a third point C 67 yd from B and 104 yd from A, with angle ACB measuring 68.3°. How far apart are A and B (to the
Nearest yard)?

Accepted Answer

A)  101 yd 
B)  128 yd 
C)  119 yd 
D)  110 yd 
A)  101 yd 
B)  128 yd 
C)  119 yd 
D)  110 yd

Question 10

Perform the indicated operation. Give answers in rectangular form expressing real and imaginary parts to four decimal
places.
-In a parallel electrical circuit, the impedance $Z$ can be calculated using the equation
$$\frac { 1 } { Z } = \left( \frac { 1 } { Z _ { 1 } } + \frac { 1 } { Z _ { 2 } } \right)$$
where $Z _ { 1 }$ and $Z _ { 2 }$ are the impedances for the branches of the circuit. The phase angle measures the phase difference between the voltage and the current in an electrical circuit. If the impedance $\mathrm { Z }$ is expressed in the form $\mathrm { a } + \mathrm { bi }$, $\theta$ can be determined by the equation $\tan \theta = \mathrm { b } / \mathrm { a }$. Determine the phase angle $\theta$ (in degrees) for a parallel circuit in which $Z _ { 1 } = 10 + 20 \mathrm { i }$ and $Z _ { 2 } = 30 + 10 \mathrm { i }$.

Accepted Answer

A)  $60 ^ { \circ }$ 
B)  $30 ^ { \circ }$ 
C)  $0 ^ { \circ }$ 
D)  $45 ^ { \circ }$ 
A)  $60 ^ { \circ }$ 
B)  $30 ^ { \circ }$ 
C)  $0 ^ { \circ }$ 
D)  $45 ^ { \circ }$

Question 11

Find the missing parts of the triangle.
-$$\begin{array} { l } 
\mathrm { A } = 65.3 ^ { \circ } \
\mathrm { a } = 2.15 \mathrm {~km} \
\mathrm {~b} = 2.25 \mathrm {~km}
\end{array}$$
If necessary, round angles to the nearest tenth and side lengths to the nearest hundredth.

Accepted Answer

A)  $\mathrm { B } = 71.9 ^ { \circ } , \mathrm { C } = 42.8 ^ { \circ } , \mathrm { c } = 1.61 \mathrm {~km}$ 
B)  $\mathrm { B } _ { 1 } = 42.8 ^ { \circ } , \mathrm { C } _ { 1 } = 71.9 ^ { \circ } , \mathrm { c } _ { 1 } = 1.61 \mathrm {~km}$ $B _ { 2 } = 6.6 ^ { \circ } , C _ { 2 } = 108.1 ^ { \circ } , c _ { 2 } = 0.27 \mathrm {~km}$ 
C)  no such triangle 
D)  $\mathrm { B } _ { 1 } = 71.9 ^ { \circ } , \mathrm { C } _ { 1 } = 42.8 ^ { \circ } , \mathrm { c } _ { 1 } = 1.61 \mathrm {~km}$
$\mathrm { B } _ { 2 } = 108.1 ^ { \circ } , \mathrm { C } _ { 2 } = 6.6 ^ { \circ } , \mathrm { c } _ { 2 } = 0.27 \mathrm {~km}$ 
A)  $\mathrm { B } = 71.9 ^ { \circ } , \mathrm { C } = 42.8 ^ { \circ } , \mathrm { c } = 1.61 \mathrm {~km}$ 
B)  $\mathrm { B } _ { 1 } = 42.8 ^ { \circ } , \mathrm { C } _ { 1 } = 71.9 ^ { \circ } , \mathrm { c } _ { 1 } = 1.61 \mathrm {~km}$ $B _ { 2 } = 6.6 ^ { \circ } , C _ { 2 } = 108.1 ^ { \circ } , c _ { 2 } = 0.27 \mathrm {~km}$ 
C)  no such triangle 
D)  $\mathrm { B } _ { 1 } = 71.9 ^ { \circ } , \mathrm { C } _ { 1 } = 42.8 ^ { \circ } , \mathrm { c } _ { 1 } = 1.61 \mathrm {~km}$
$\mathrm { B } _ { 2 } = 108.1 ^ { \circ } , \mathrm { C } _ { 2 } = 6.6 ^ { \circ } , \mathrm { c } _ { 2 } = 0.27 \mathrm {~km}$

Question 12

Give the rectangular coordinates for the point.
-$$\left( - 5 , \frac { 5 \pi } { 3 } \right)$$

Accepted Answer

A)  $\left( \frac { 5 } { 2 } , - \frac { 5 } { 2 } \right)$ 
B)  $\left( \frac { 5 \sqrt { 3 } } { 2 } , - \frac { 5 } { 2 } \right)$ 
C)  $\left( - \frac { 5 } { 2 } , \frac { 5 \sqrt { 3 } } { 2 } \right)$ 
D)  $\left( - \frac { 5 } { 2 } , \frac { 5 } { 2 } \right)$ 
A)  $\left( \frac { 5 } { 2 } , - \frac { 5 } { 2 } \right)$ 
B)  $\left( \frac { 5 \sqrt { 3 } } { 2 } , - \frac { 5 } { 2 } \right)$ 
C)  $\left( - \frac { 5 } { 2 } , \frac { 5 \sqrt { 3 } } { 2 } \right)$ 
D)  $\left( - \frac { 5 } { 2 } , \frac { 5 } { 2 } \right)$

Question 13

Find all specified roots.
-Eleventh roots of 1.

Accepted Answer

A)  $1 , \operatorname { cis } \frac { \pi } { 11 } , \operatorname { cis } \frac { 2 \pi } { 11 } , \operatorname { cis } \frac { 3 \pi } { 11 } , \operatorname { cis } \frac { 4 \pi } { 11 } , \operatorname { cis } \frac { 5 \pi } { 11 } , \operatorname { cis } \frac { 6 \pi } { 11 } , \operatorname { cis } \frac { 7 \pi } { 11 } , \operatorname { cis } \frac { 8 \pi } { 11 } , \operatorname { cis } \frac { 9 \pi } { 11 } , \operatorname { cis } \frac { 10 \pi } { 11 }$ 
B)  $1 , \operatorname { cis } \frac { 2 \pi } { 11 } , \operatorname { cis } \frac { 4 \pi } { 11 } , \operatorname { cis } \frac { 6 \pi } { 11 } , \operatorname { cis } \frac { 8 \pi } { 11 } , \operatorname { cis } \frac { 10 \pi } { 11 }$ 
C)  $1 , \operatorname { cis } \frac { 2 \pi } { 11 } , \operatorname { cis } \frac { 4 \pi } { 11 } , \operatorname { cis } \frac { 6 \pi } { 11 } , \operatorname { cis } \frac { 8 \pi } { 11 } , \operatorname { cis } \frac { 10 \pi } { 11 } , \operatorname { cis } \frac { 12 \pi } { 11 } , \operatorname { cis } \frac { 14 \pi } { 11 } , \operatorname { cis } \frac { 16 \pi } { 11 } , \operatorname { cis } \frac { 18 \pi } { 11 } , \operatorname { cis } \frac { 20 \pi } { 11 }$ 
D)  $1 , \operatorname { cis } \frac { 2 \pi } { 11 } , \operatorname { cis } \frac { 4 \pi } { 11 } , \operatorname { cis } \frac { 6 \pi } { 11 } , \operatorname { cis } \frac { 8 \pi } { 11 } , \operatorname { cis } \frac { 10 \pi } { 11 } , \operatorname { cis } \frac { 12 \pi } { 11 } , \operatorname { cis } \frac { 14 \pi } { 11 } , \operatorname { cis } \frac { 16 \pi } { 11 } , \operatorname { cis } \frac { 18 \pi } { 11 } , - 1$ 
A)  $1 , \operatorname { cis } \frac { \pi } { 11 } , \operatorname { cis } \frac { 2 \pi } { 11 } , \operatorname { cis } \frac { 3 \pi } { 11 } , \operatorname { cis } \frac { 4 \pi } { 11 } , \operatorname { cis } \frac { 5 \pi } { 11 } , \operatorname { cis } \frac { 6 \pi } { 11 } , \operatorname { cis } \frac { 7 \pi } { 11 } , \operatorname { cis } \frac { 8 \pi } { 11 } , \operatorname { cis } \frac { 9 \pi } { 11 } , \operatorname { cis } \frac { 10 \pi } { 11 }$ 
B)  $1 , \operatorname { cis } \frac { 2 \pi } { 11 } , \operatorname { cis } \frac { 4 \pi } { 11 } , \operatorname { cis } \frac { 6 \pi } { 11 } , \operatorname { cis } \frac { 8 \pi } { 11 } , \operatorname { cis } \frac { 10 \pi } { 11 }$ 
C)  $1 , \operatorname { cis } \frac { 2 \pi } { 11 } , \operatorname { cis } \frac { 4 \pi } { 11 } , \operatorname { cis } \frac { 6 \pi } { 11 } , \operatorname { cis } \frac { 8 \pi } { 11 } , \operatorname { cis } \frac { 10 \pi } { 11 } , \operatorname { cis } \frac { 12 \pi } { 11 } , \operatorname { cis } \frac { 14 \pi } { 11 } , \operatorname { cis } \frac { 16 \pi } { 11 } , \operatorname { cis } \frac { 18 \pi } { 11 } , \operatorname { cis } \frac { 20 \pi } { 11 }$ 
D)  $1 , \operatorname { cis } \frac { 2 \pi } { 11 } , \operatorname { cis } \frac { 4 \pi } { 11 } , \operatorname { cis } \frac { 6 \pi } { 11 } , \operatorname { cis } \frac { 8 \pi } { 11 } , \operatorname { cis } \frac { 10 \pi } { 11 } , \operatorname { cis } \frac { 12 \pi } { 11 } , \operatorname { cis } \frac { 14 \pi } { 11 } , \operatorname { cis } \frac { 16 \pi } { 11 } , \operatorname { cis } \frac { 18 \pi } { 11 } , - 1$

Question 14

Determine the number of triangles ABC possible with the given parts.
-$$\mathrm { b } = 41 , \mathrm { c } = 51 , \mathrm {~B} = 100 ^ { \circ }$$

Accepted Answer

A)  3 
B)  0 
C)  2 
D)  1 
A)  3 
B)  0 
C)  2 
D)  1

Question 15

Solve the problem.
-Two tracking stations are on the equator 146 miles apart. A weather balloon is located on a bearing of $\mathrm { N } 43 ^ { \circ } \mathrm { E }$ from the western station and a bearing of $\mathrm { N } 23 ^ { \circ } \mathrm { E }$ from the eastern station. How far, to the nearest mile, is the balloon from the western station? Round to the nearest mile.

Accepted Answer

A)  $393 \mathrm { mi }$ 
B)  $381 \mathrm { mi }$ 
C)  $402 \mathrm { mi }$ 
D)  $390 \mathrm { mi }$ 
A)  $393 \mathrm { mi }$ 
B)  $381 \mathrm { mi }$ 
C)  $402 \mathrm { mi }$ 
D)  $390 \mathrm { mi }$

Question 16

Use the parallelogram rule to find the magnitude of the resultant force for the two forces shown in the figure. Round to
one decimal place.
-A hot-air balloon is rising vertically $14 \mathrm { ft } / \mathrm { sec }$ while the wind is blowing horizontally at $2 \mathrm { ft } / \mathrm { sec }$. Find the angle that the balloon makes with the horizontal.

Accepted Answer

A)  $37.6 ^ { \circ }$ 
B)  $8.1 ^ { \circ }$ 
C)  $56.7 ^ { \circ }$ 
D)  $81.9 ^ { \circ }$ 
A)  $37.6 ^ { \circ }$ 
B)  $8.1 ^ { \circ }$ 
C)  $56.7 ^ { \circ }$ 
D)  $81.9 ^ { \circ }$

Question 17

Assume a triangle ABC has standard labeling. Determine whether SAA, ASA, SSA, SAS, or SSS is given. Then decide
whether the law of sines or the law of cosines should be used to begin solving the triangle.
-a, b, and B

Accepted Answer

A)  ASA; law of cosines 
B)  SSA; law of sines 
C)  ASA; law of sines 
D)  SSA; law of cosines 
A)  ASA; law of cosines 
B)  SSA; law of sines 
C)  ASA; law of sines 
D)  SSA; law of cosines

Question 18

Find the area of triangle ABC with the given parts. Round to the nearest tenth when necessary.
-A painter needs to cover a triangular region 63 meters by 67 meters by 71 meters. A can of paint covers 70 square meters. How many cans will be needed?

Accepted Answer

A)  14 cans 
B)  $3 \mathrm { cans }$ 
C)  315 cans 
D)  28 cans 
A)  14 cans 
B)  $3 \mathrm { cans }$ 
C)  315 cans 
D)  28 cans

Question 19

Vector v has the given magnitude and direction. Find the horizontal or vertical component of v, as indicated, if $\theta$ is the
direction angle of v from the horizontal. Round to the nearest tenth when necessary.
-$\alpha = 28.6 ^ { \circ } , | \mathbf { v } | = 411 ;$ Find the vertical component of $\mathbf { v }$

Accepted Answer

A)  $164.2$ 
B)  $196.7$ 
C)  $360.9$ 
D)  $557.6$ 
A)  $164.2$ 
B)  $196.7$ 
C)  $360.9$ 
D)  $557.6$

Question 20

Find the indicated vector.
-Let $\mathbf { u } = \langle 4 , - 1 \rangle$. Find $- 8 \mathbf { u }$.

Accepted Answer

A)  $\langle 32 , - 8 \rangle$ 
B)  $\langle - 32,8 \rangle$ 
C)  $\langle - 32 , - 8 \rangle$ 
D)  $\langle 32,8 \rangle$ 
A)  $\langle 32 , - 8 \rangle$ 
B)  $\langle - 32,8 \rangle$ 
C)  $\langle - 32 , - 8 \rangle$ 
D)  $\langle 32,8 \rangle$

Find the missing parts of the triangle. Round to the nearest tenth when necessary or to the nearest minute as appropriate. - a=7.2. =13.7. =15.6.

Find a rectangular equation for the plane curve defined by the parametric equations. - $x = \sqrt { t } , y = 2 t + 5$

Find the missing parts of the triangle. - =96. =15.2 =30.4 If necessary, round angles and side lengths to the nearest tenth.

Find the missing parts of the triangle. Round to the nearest tenth when necessary or to the nearest minute as appropriate. - =105. =4.7 =8.3

Determine whether the pair of vectors is orthogonal. - $\langle - 10 , \sqrt { 3 } \rangle , \langle - 2 \sqrt { 3 } , - 30 \rangle$

Find the missing parts of the triangle. - A=44.2 a=51.82 b=63.64 If necessary, round angles and side lengths to the nearest hundredth.

Find the given power. Write answer in rectangular form. - $[ - 4 + 4 i \sqrt { 3 } ] ^ { 3 }$

Find the indicated angle or side. Give an exact answer. -Find the measure of angle A in degrees.

Find the area of triangle ABC with the given parts. Round to the nearest tenth when necessary. -Two points A and B are on opposite sides of a building. A surveyor chooses a third point C 67 yd from B and 104 yd from A, with angle ACB measuring 68.3°. How far apart are A and B (to the Nearest yard)?

Find the missing parts of the triangle. - =65. =2.15 =2.25 If necessary, round angles to the nearest tenth and side lengths to the nearest hundredth.

Give the rectangular coordinates for the point. - $\left( - 5 , \frac { 5 \pi } { 3 } \right)$

Find all specified roots. -Eleventh roots of 1.

Determine the number of triangles ABC possible with the given parts. - $\mathrm { b } = 41 , \mathrm { c } = 51 , \mathrm {~B} = 100 ^ { \circ }$

Assume a triangle ABC has standard labeling. Determine whether SAA, ASA, SSA, SAS, or SSS is given. Then decide whether the law of sines or the law of cosines should be used to begin solving the triangle. -a, b, and B

Find the area of triangle ABC with the given parts. Round to the nearest tenth when necessary. -A painter needs to cover a triangular region 63 meters by 67 meters by 71 meters. A can of paint covers 70 square meters. How many cans will be needed?

Find the indicated vector. -Let $\mathbf { u } = \langle 4 , - 1 \rangle$ . Find $- 8 \mathbf { u }$ .

Review of Basic Concepts

Equations and Inequalities

Graphs and Functions

Polynomial and Rational Functions

Inverse, Exponential, and Logarithmic Functions

Trigonometric Functions

The Circular Functions and Their Graphs

Trigonometric Identities and Equations

Systems and Matrices

Analytic Geometry

Further Topics in Algebra

Filters

Exam 9: Applications of Trigonometry