Exam 7: The Circular Functions and Their Graphs
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Graph the function over a one-period interval.
-The weekly sales in thousands of items of a product has a seasonal sales record approximated by which week(s) will the sales equal 69,770 items?
(Multiple Choice)
4.8/5  (38)
(38)
Convert the radian measure to degrees. Give answer using decimal degrees to the nearest hundredth. Us
-
(Multiple Choice)
4.9/5  (31)
(31)
Assume that the cities lie on the same north-south line and that the radius of the earth is 6400 km.
-A pulley with a diameter of 28 inches is driven by a belt which is moving . To the nearest unit, how many revolutions per minute are made by the pulley?
(Multiple Choice)
4.9/5  (33)
(33)
Solve the problem
-A pulley of radius rotates 15 times in . Find the angular speed of the pulley.
(Multiple Choice)
4.8/5  (28)
(28)
Find the area of a sector of a circle having radius r and central angle . If necessary, express the answer to the nearest
tenth.
-
(Multiple Choice)
5.0/5  (39)
(39)
Find the exact value of s in the given interval that has the given circular function value.
-
(Multiple Choice)
4.8/5  (40)
(40)
The figure shows an angle in standard position with its terminal side intersecting the unit circle. Evaluate the indicated
circular function value of
-Find
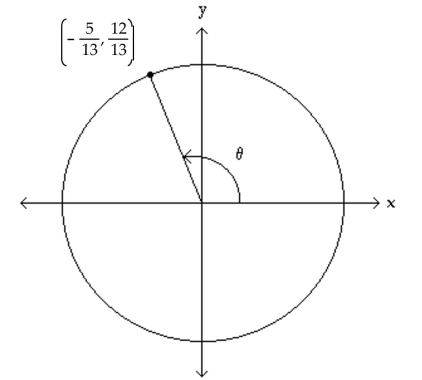
(Multiple Choice)
4.9/5  (33)
(33)
Use the formula to find the value of the missing variable. Give an exact answer unless otherwise indicated.
- radian,
(Multiple Choice)
4.9/5  (34)
(34)
Find the exact values of s in the given interval that satisfy the given condition.
-
(Multiple Choice)
4.7/5  (42)
(42)
The function graphed is of the form y Determine the equation of the graph.
-The chart represents the amount of fuel consumed by a machine used in manufacturing. The machine is turned on at the beginning of the day, takes a certain amount of time to reach its full power (the point at which it uses the most fuel per hour), runs for a certain number of hours, and is shut off at the end of the work day. The fuel usage per hour of the machine is represented by a periodic function. When does the machine first reach its full power?
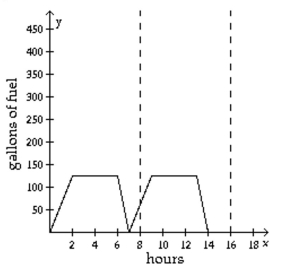
(Multiple Choice)
4.8/5  (35)
(35)
The function graphed is of the form y Determine the equation of the graph.
-For an electrical circuit, the voltage is modeled by , where is the time in seconds. How many cycles are completed in one second?
(Multiple Choice)
4.9/5  (34)
(34)
Find the exact value of s in the given interval that has the given circular function value.
-
(Multiple Choice)
4.9/5  (22)
(22)
Convert the degree measure to radians, correct to four decimal places.
-
(Multiple Choice)
4.8/5  (34)
(34)
Find the value of s in the interval [ /2] that makes the statement true. Round to four decimal places.
-
(Multiple Choice)
4.9/5  (31)
(31)
The function graphed is of the form y Determine the equation of the graph.
-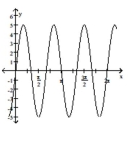
(Multiple Choice)
4.9/5  (38)
(38)
Determine the equation of the graph.
-A rotating beacon is located from a wall. The distance from the beacon to the point on the wall where the beacon is aimed is given by
where is time measured in seconds since the beacon started rotating. Find a for seconds. Ro your answer to the nearest hundredth.
(Multiple Choice)
4.9/5  (41)
(41)
Showing 21 - 40 of 286
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)