Exam 7: The Circular Functions and Their Graphs
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Find the area of a sector of a circle having radius r and central angle . If necessary, express the answer to the nearest
tenth.
- Find the radius of a circle in which a central angle of radian determines a sector of area 57 square meters. Round to the nearest hundredth.
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem
-An object is spinning around a circle with a radius of 24 centimeters. If in 14 seconds a central angle of radian has been covered, what is the linear speed of the object?
(Multiple Choice)
4.9/5  (37)
(37)
Assume that the cities lie on the same north-south line and that the radius of the earth is 6400 km.
-Find the radius (to the nearest hundredth of a millimeter) of a pulley if rotating the pulley raises the pulley .
(Multiple Choice)
5.0/5  (37)
(37)
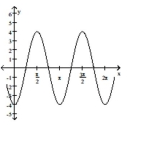
The function graphed is of the form y Determine the equation of the graph.
-
(Multiple Choice)
4.8/5  (48)
(48)
Find the area of a sector of a circle having radius r and central angle . If necessary, express the answer to the nearest
tenth.
-Find the measure (in radians) of a central angle of a sector of area 56 square inches in a circle of radius 8 inches. Round to the nearest hundredth.
(Multiple Choice)
4.8/5  (33)
(33)
Graph the function over a one-period interval.
-The temperature in Fairbanks is approximated by where is the temperature on day , with corresponding to Jan. 1 and correspondin; to Dec. 31. Estimate the temperature on day 31.
(Multiple Choice)
4.8/5  (33)
(33)
The function graphed is of the form where d is the least possible
positive value. Determine the equation of the graph.
-
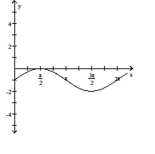
(Multiple Choice)
4.8/5  (42)
(42)
Graph the function over a one-period interval.
-A coil of wire ro tating in a magnetic field induces a voltage given by
where is time in seconds. Find the smallest positive time to produce a voltage of .
(Multiple Choice)
4.9/5  (38)
(38)
The function graphed is of the form y Determine the equation of the graph.
-A weight attached to a spring is pulled down 7 inches below the equilibrium position. Assuming that the period of the system is second, determine a trigonometric model that gives the position of the weight at time seconds.
(Multiple Choice)
4.9/5  (39)
(39)
Convert the degree measure to radians. Leave answer as a multiple of
-
(Multiple Choice)
4.7/5  (32)
(32)
Showing 41 - 60 of 286
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)