Exam 7: The Circular Functions and Their Graphs
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
Determine the equation of the graph.
-The position of a weight attached to a spring is inches after seconds. What is the maximum height that the weight reaches above the equilibrium position and when does it first reach the maximum height? Round values to two decimal places, if necessary.
(Multiple Choice)
4.8/5  (23)
(23)
Is it correct to say that the value of ta ? Explain your answer.
(Short Answer)
4.9/5  (33)
(33)
The function graphed is of the form y Determine the equation of the graph.
-A weight attached to a spring is pulled down 3 inches below the equilibrium position. Assuming that the frequency of the system is cycles per second, determine a trigonometric model that gives the position of the weight at time second.
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem
-Two pulleys of diameters and are connected by a belt. The larger pulley rotates 31 times per min. Find the angular speed of the smaller pulley.
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem
-A wheel is rotating at 8 radians per sec, and the wheel has a 56 -inch diameter. To the nearest foot per minute, what is the speed of a point on the rim?
(Multiple Choice)
4.8/5  (41)
(41)
Use a table or a calculator to evaluate the function. Round to four decimal places.
-
(Multiple Choice)
4.9/5  (36)
(36)
The function graphed is of the form y Determine the equation of the graph.
-The chart represents the amount of fuel consumed by a machine used in manufacturing. The machine is turned on at the beginning of the day, takes a certain amount of time to reach its full power (the point at which it uses the most fuel per hour), runs for a certain number of hours, and is shut off at the end of the work day. The fuel usage per hour of the machine is represented by a periodic function. What is the period in hours of this function?
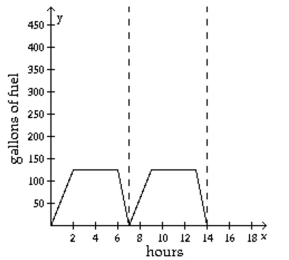
(Multiple Choice)
4.8/5  (41)
(41)
The figure shows an angle in standard position with its terminal side intersecting the unit circle. Evaluate the indicated
circular function value of
-Find
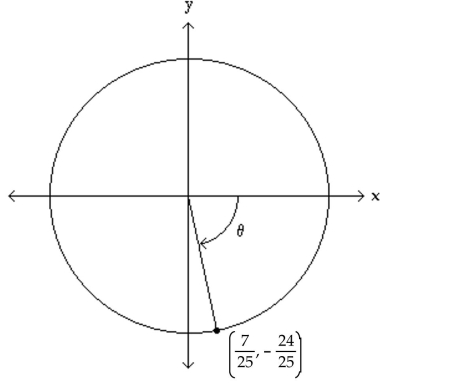
(Multiple Choice)
4.8/5  (32)
(32)
Find the value of s in the interval [ /2] that makes the statement true. Round to four decimal places.
-
(Multiple Choice)
4.8/5  (34)
(34)
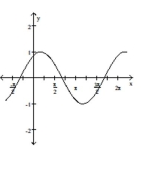
The function graphed is of the form where d is the least possible
positive value. Determine the equation of the graph.
-
(Multiple Choice)
4.9/5  (37)
(37)
Find the exact values of s in the given interval that satisfy the given condition.
-
(Multiple Choice)
4.9/5  (35)
(35)
The figure shows an angle in standard position with its terminal side intersecting the unit circle. Evaluate the indicated
circular function value of
-Find .
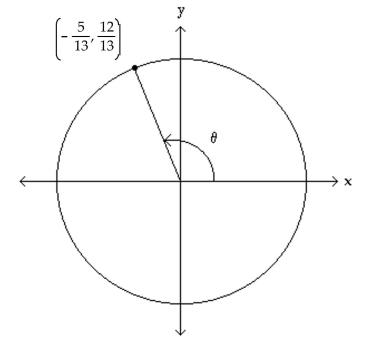
(Multiple Choice)
4.9/5  (31)
(31)
Showing 141 - 160 of 286
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)