Exam 7: The Circular Functions and Their Graphs
Exam 1: Review of Basic Concepts639 Questions
Exam 2: Equations and Inequalities496 Questions
Exam 3: Graphs and Functions522 Questions
Exam 4: Polynomial and Rational Functions508 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Trigonometric Functions297 Questions
Exam 7: The Circular Functions and Their Graphs286 Questions
Exam 8: Trigonometric Identities and Equations492 Questions
Exam 9: Applications of Trigonometry447 Questions
Exam 10: Systems and Matrices507 Questions
Exam 11: Analytic Geometry217 Questions
Exam 12: Further Topics in Algebra348 Questions
Select questions type
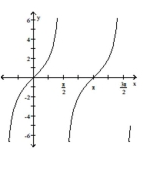
The function graphed is of the form y etermine the equation of the graph.
-
(Multiple Choice)
4.9/5  (40)
(40)
Determine the equation of the graph.
-The position of a weight attached to a spring is inches after seconds. When does the weight first reach its maximum height?
(Multiple Choice)
4.8/5  (35)
(35)
Use the formula v to find the value of the missing variable. Give an exact answer unless otherwise indicated.
- per sec, (Round to four decimal places when necessary.)
(Multiple Choice)
4.8/5  (30)
(30)
Convert the radian measure to degrees. Round to the nearest hundredth if necessary.
-
(Multiple Choice)
4.9/5  (35)
(35)
Find the exact values of s in the given interval that satisfy the given condition.
-
(Multiple Choice)
4.8/5  (39)
(39)
Convert the radian measure to degrees. Round to the nearest hundredth if necessary.
-
(Multiple Choice)
4.8/5  (33)
(33)
Find the length of an arc intercepted by a central angle in a circle of radius r. Round your answer to 1 decimal place.
- radians
(Multiple Choice)
4.9/5  (27)
(27)
Find the area of a sector of a circle having radius r and central angle . If necessary, express the answer to the nearest
tenth.
- radians
(Multiple Choice)
4.9/5  (31)
(31)
The figure shows an angle in standard position with its terminal side intersecting the unit circle. Evaluate the indicated
circular function value of
-Find
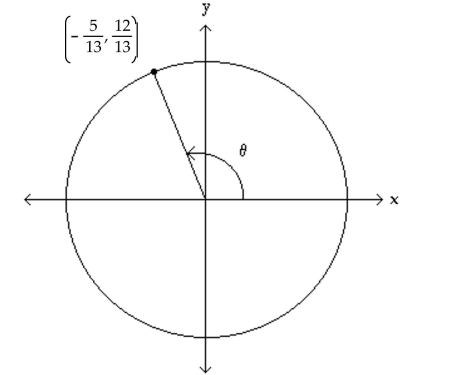
(Multiple Choice)
4.9/5  (34)
(34)
Find the area of a sector of a circle having radius r and central angle . If necessary, express the answer to the nearest
tenth.
-What is the difference in area covered by a single 5 -inch windshield wiper operating with a central angle of compared to a pair of 5 -inch wipers operating together each having a central angle of ? Round to the nearest hundredth.
(Multiple Choice)
4.9/5  (42)
(42)
Assume that the cities lie on the same north-south line and that the radius of the earth is 6400 km.
-A pulley rotates through in one minute. How many rotations (to the nearest tenth of a rotation) does the pulley make in an hour?
(Multiple Choice)
4.8/5  (41)
(41)
Find the length of an arc intercepted by a central angle in a circle of radius r. Round your answer to 1 decimal place.
- radians
(Multiple Choice)
4.8/5  (32)
(32)
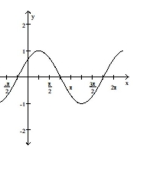
The function graphed is of the form where d is the least possible
positive value. Determine the equation of the graph.
-
(Multiple Choice)
4.7/5  (34)
(34)
The figure shows an angle in standard position with its terminal side intersecting the unit circle. Evaluate the indicated
circular function value of
-Find .
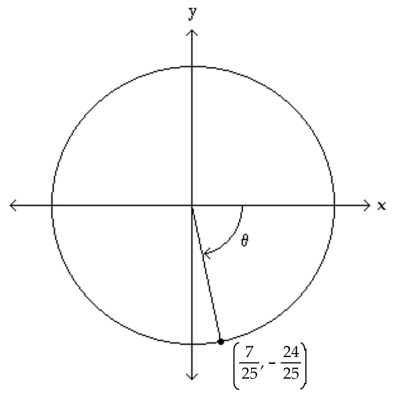
(Multiple Choice)
4.9/5  (36)
(36)
Showing 161 - 180 of 286
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)