Exam 6: Analytic Trigonometry

Choose the one alternative that best completes the statement or answers the question. Complete the identity. - $\sin ^ { 2 } \theta + \tan ^ { 2 } \theta + \cos ^ { 2 } \theta = \text { ? }$

Choose the one alternative that best completes the statement or answers the question. Complete the identity. - $\sin ( \pi - \theta ) = \text { ? }$

Find the inverse function f-1 of the function f. - $f ( x ) = 4 \tan ( 9 x )$

Choose the one alternative that best completes the statement or answers the question. Complete the identity. - $\frac { \sin ^ { 2 } \theta - 1 } { \sin \theta + 1 } = \text { ? }$

Find the exact value of the expression. Do not use a calculator. - $\tan ^ { - 1 } \left[ \tan \left( - \frac { \pi } { 8 } \right) \right]$

Solve the equation. Give a general formula for all the solutions. - $\sin \theta = 1$

Solve the problem. -On a Touch-Tone phone, each button produces a unique sound. The sound produced is the sum of two tones, gi $y = \sin ( 2 \pi l t )$ and $y = \sin ( 2 \pi h t )$ where $l$ and h are the low and high frequencies (cycles per second) shown on the illustration. 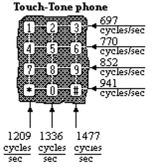The sound produced is thus given by $y = \sin ( 2 \pi l t ) + \sin ( 2 \pi h t )$ Write the sound emitted by touching the 4 key as a product of sines and cosines.

Choose the one alternative that best completes the statement or answers the question. - $\sin ^ { 2 } x + 8 \sin x + 16 = 0$

Find the exact value of the expression. Do not use a calculator. - $\sin ^ { - 1 } \left[ \sin \left( \frac { 6 \pi } { 7 } \right) \right]$

Choose the one alternative that best completes the statement or answers the question. - $3 \cos ^ { 2 } x + 2 \cos x = 1$

Find the exact value of the expression. - $\tan 75 ^ { \circ }$

Choose the one alternative that best completes the statement or answers the question. Express the product as a sum containing only sines or cosines. - $\sin ( 3 \theta ) \cos ( 4 \theta )$

Write the word or phrase that best completes each statement or answers the question. Establish the identity. - $\frac { \cot ^ { 2 } x } { \csc x + 1 } = \frac { 1 - \sin x } { \sin x }$

Write the word or phrase that best completes each statement or answers the question. Solve the problem. -The seasonal variation in the length of daylight can be represented by a sine function. For example, the daily number of hours of daylight in a certain city in the U.S. can be given by $h = \frac { 41 } { 4 } + \frac { 5 } { 3 } \sin \frac { 2 \pi x } { 365 }$ , where $x$ is the number of days after March 21 ( disregarding leap year). On what day(s) will there be about 10 hours of daylight?

Choose the one alternative that best completes the statement or answers the question. Complete the identity. - $\frac { 7 + 7 \sin \theta } { - 5 \cos \theta } = \text { ? }$

Choose the one alternative that best completes the statement or answers the question. Complete the identity. - $\frac { \sin \theta } { \cos \theta } + \frac { \cos \theta } { \sin \theta } = \text { ? }$

Choose the one alternative that best completes the statement or answers the question. Use a graphing utility to solve the equation on the interval 0° x < 360°. Express the solution(s) rounded to one decimal place. - $2 + 13 \sin x = 14 \cos ^ { 2 } x$

Write the word or phrase that best completes each statement or answers the question. Establish the identity. - $\frac { 1 + \csc x } { \sec x } = \cos x + \cot x$

Find the domain of the function f and of its inverse function f-1. - $f ( x ) = 6 \tan x + 10$

Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. - $\sec \left( \tan ^ { - 1 } \frac { \sqrt { 3 } } { 3 } \right)$