Exam 3: Polynomial and Rational Functions
Exam 1: Functions and Their Graphs297 Questions
Exam 2: Linear and Quadratic Functions302 Questions
Exam 3: Polynomial and Rational Functions354 Questions
Exam 4: Exponential and Logarithmic Functions517 Questions
Exam 5: Trigonometric Functions354 Questions
Exam 6: Analytic Trigonometry342 Questions
Exam 7: Applications of Trigonometric Functions105 Questions
Exam 8: Polar Coordinates; Vectors253 Questions
Exam 9: Analytic Geometry200 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability115 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Foundations: a Prelude to Functions234 Questions
Exam 15: Graphing Utilities29 Questions
Select questions type
Use the x-intercepts to find the intervals on which the graph of f is above and below the x-axis.
-
(Multiple Choice)
4.8/5  (37)
(37)
Use the Factor Theorem to determine whether x - c is a factor of f. If it is, write f in factored form, that is, write f in the
form f(x) = (x - c)(quotient).
-
(Multiple Choice)
4.9/5  (36)
(36)
Give the equation of the horizontal asymptote, if any, of the function.
-
(Multiple Choice)
4.8/5  (43)
(43)
Write the word or phrase that best completes each statement or answers the question.
The equation has a solution r in the interval indicated. Approximate this solution correct to two decimal places.
-
(Short Answer)
4.8/5  (40)
(40)
Form a polynomial whose zeros and degree are given. Use a leading coefficient of 1.
-Zeros: ; degree 4
(Multiple Choice)
4.8/5  (38)
(38)
State whether the function is a polynomial function or not. If it is, give its degree. If it is not, tell why not.
-
(Multiple Choice)
4.8/5  (38)
(38)
Use transformations of the graph o to graph the function.
-
(Multiple Choice)
4.9/5  (28)
(28)
Give the maximum number of zeros the polynomial function may have. Use Descarte's Rule of Signs to determine how
many positive and how many negative zeros it may have.
-
(Multiple Choice)
4.8/5  (34)
(34)
Use the Intermediate Value Theorem to determine whether the polynomial function has a zero in the given interval.
-
(Multiple Choice)
4.9/5  (28)
(28)
Find the indicated intercept(s) of the graph of the function.
- -intercept of
(Multiple Choice)
4.7/5  (32)
(32)
Find the indicated intercept(s) of the graph of the function.
- -intercept of
(Multiple Choice)
4.8/5  (34)
(34)
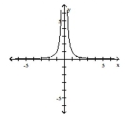
Solve the problem.
-Decide which of the rational functions might have the given graph.
(Multiple Choice)
4.8/5  (41)
(41)
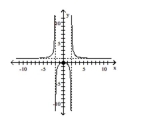
Use the graph to determine the domain and range of the function.
-
(Multiple Choice)
4.8/5  (40)
(40)
Form a polynomial whose zeros and degree are given. Use a leading coefficient of 1.
-Zeros: 0, - 7, 6; degree 3
(Multiple Choice)
4.8/5  (43)
(43)
Showing 321 - 340 of 354
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)