Exam 3: Polynomial and Rational Functions
Exam 1: Functions and Their Graphs297 Questions
Exam 2: Linear and Quadratic Functions302 Questions
Exam 3: Polynomial and Rational Functions354 Questions
Exam 4: Exponential and Logarithmic Functions517 Questions
Exam 5: Trigonometric Functions354 Questions
Exam 6: Analytic Trigonometry342 Questions
Exam 7: Applications of Trigonometric Functions105 Questions
Exam 8: Polar Coordinates; Vectors253 Questions
Exam 9: Analytic Geometry200 Questions
Exam 10: Systems of Equations and Inequalities235 Questions
Exam 11: Sequences; Induction; the Binomial Theorem238 Questions
Exam 12: Counting and Probability115 Questions
Exam 13: A Preview of Calculus: the Limit, Derivative, and Integral of a Function145 Questions
Exam 14: Foundations: a Prelude to Functions234 Questions
Exam 15: Graphing Utilities29 Questions
Select questions type
Use transformations of the graph o to graph the function.
-
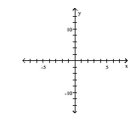
(Multiple Choice)
4.8/5  (37)
(37)
Use the Factor Theorem to determine whether x - c is a factor of f(x).
-
(Multiple Choice)
4.9/5  (36)
(36)
Use the Factor Theorem to determine whether x - c is a factor of f(x).
-
(Multiple Choice)
4.8/5  (37)
(37)
Use the Factor Theorem to determine whether x - c is a factor of f(x).
-
(Multiple Choice)
4.8/5  (40)
(40)
Use transformations of the graph o to graph the function.
-
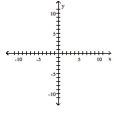
(Multiple Choice)
4.8/5  (33)
(33)
Give the equation of the oblique asymptote, if any, of the function.
-
(Multiple Choice)
4.7/5  (38)
(38)
Use Descartes' Rule of Signs and the Rational Zeros Theorem to find all the real zeros of the polynomial function. Use the
zeros to factor f over the real numbers.
-
(Multiple Choice)
4.8/5  (42)
(42)
Use the graph to determine the domain and range of the function.
-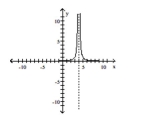
(Multiple Choice)
4.7/5  (45)
(45)
State whether the function is a polynomial function or not. If it is, give its degree. If it is not, tell why not.
-
(Multiple Choice)
4.7/5  (35)
(35)
Find all zeros of the function and write the polynomial as a product of linear factors.
-
(Multiple Choice)
4.9/5  (37)
(37)
For the polynomial, list each real zero and its multiplicity. Determine whether the graph crosses or touches the x-axis at
each x -intercept.
-
(Multiple Choice)
4.9/5  (42)
(42)
Write the word or phrase that best completes each statement or answers the question.
Analyze the graph of the given function f as follows:
(a) Determine the end behavior: find the power function that the graph of f resembles for large values of |x|.
(b) Find the x- and y-intercepts of the graph.
(c) Determine whether the graph crosses or touches the x-axis at each x-intercept.
(d) Graph f using a graphing utility.
(e) Use the graph to determine the local maxima and local minima, if any exist. Round turning points to two decimal places.
(f) Use the information obtained in (a) - (e) to draw a complete graph of f by hand. Label all intercepts and turning points.
(g) Find the domain of f. Use the graph to find the range of f.
(h) Use the graph to determine where f is increasing and where f is decreasing.
-
(Essay)
4.8/5  (43)
(43)
Give the maximum number of zeros the polynomial function may have. Use Descarte's Rule of Signs to determine how
many positive and how many negative zeros it may have.
-
(Multiple Choice)
4.7/5  (30)
(30)
Give the maximum number of zeros the polynomial function may have. Use Descarte's Rule of Signs to determine how
many positive and how many negative zeros it may have.
-
(Multiple Choice)
4.9/5  (29)
(29)
Showing 21 - 40 of 354
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)