Exam 3: Polynomial and Rational Functions

Write the word or phrase that best completes each statement or answers the question. -The amount of water (in gallons) in a leaky bathtub is given in the table below. Using a graphing utility, fit the data to a third degree polynomial (or a cubic). Then approximate the time at which there is maximum amount Of water in the tub, and estimate the time when the water runs out of the tub. Express all your answers rounded To two decimal places. t (in minutes) 0 1 2 3 4 5 6 7 (in gallons) 20 26 45 63 86 94 90 67

Solve the inequality. - $x ^ { 2 } - 3 x \geq - 2$

Find the vertical asymptotes of the rational function. - $h ( x ) = \frac { x + 11 } { x ^ { 2 } - 16 x }$

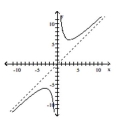
Use the graph to determine the domain and range of the function. -

Solve the inequality. - $x ^ { 2 } - 5 x \leq 0$

Find the x- and y-intercepts of f. - $f ( x ) = ( x + 5 ) ( x - 4 ) ( x + 4 )$

Solve the equation in the real number system. - $x ^ { 3 } + 3 x ^ { 2 } - 8 x + 10 = 0$

Form a polynomial f(x) with real coefficients having the given degree and zeros. -Degree: 4 ; zeros: $- 1,2$ , and $1 - 2 i$ .

Find the vertical asymptotes of the rational function. - $f ( x ) = \frac { - 2 x ( x + 2 ) } { 4 x ^ { 2 } - 5 x - 9 }$

Solve the inequality. - $\frac { ( x - 3 ) ( x + 3 ) } { x } \leq 0$

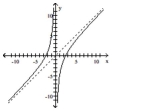
Use the graph to find the vertical asymptotes, if any, of the function. -

Find the power function that the graph of f resembles for large values of |x|. - $f ( x ) = 3 x - x ^ { 3 }$

Solve the inequality. - $x ^ { 4 } - 12 x ^ { 2 } - 64 > 0$

Find the indicated intercept(s) of the graph of the function. - $x$ -intercepts of $f ( x ) = \frac { 2 x + 5 } { x - 5 }$

Find the vertical asymptotes of the rational function. - $h ( x ) = \frac { 6 x } { x + 2 }$

Solve the inequality. - $x ^ { 2 } - 64 > 0$

Graph the function using transformations. - $f ( x ) = \frac { 1 } { x - 3 } + 1$

Write the word or phrase that best completes each statement or answers the question. Analyze the graph of the given function f as follows: (a) Determine the end behavior: find the power function that the graph of f resembles for large values of |x|. (b) Find the x- and y-intercepts of the graph. (c) Determine whether the graph crosses or touches the x-axis at each x-intercept. (d) Graph f using a graphing utility. (e) Use the graph to determine the local maxima and local minima, if any exist. Round turning points to two decimal places. (f) Use the information obtained in (a) - (e) to draw a complete graph of f by hand. Label all intercepts and turning points. (g) Find the domain of f. Use the graph to find the range of f. (h) Use the graph to determine where f is increasing and where f is decreasing. - $f ( x ) = x ^ { 2 } \left( x ^ { 2 } - 4 \right) ( x + 4 )$

Solve the problem. -The revenue achieved by selling x graphing calculators is figured to be x(39 - 0.2x) dollars. The cost of each calculator is $27. How many graphing calculators must be sold to make a profit (revenue - cost) of at least $160.00?

Find the power function that the graph of f resembles for large values of |x|. - $f ( x ) = ( x - 3 ) ^ { 3 }$