Exam 11: Sequences, Induction, and Probability

Express the repeating decimal as a fraction in lowest terms. - $0 . \overline { 2 } = \frac { 2 } { 10 } + \frac { 2 } { 100 } + \frac { 2 } { 1,000 } + \frac { 2 } { 10,000 } \ldots$

Expand a Binomial Raised to a Power - $( x + 2 ) ^ { 3 }$

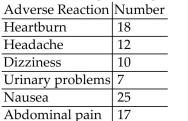
Probability 1 Compute Empirical Probability -During clinical trials of a new drug intended to reduce the risk of heart attack, the following data indicate the occurrence of adverse reactions among 1000 adult male trial members. What is the probability that an adult male using the drug will experience nausea?

Find the indicated sum. Use the formula for the sum of the first n terms of a geometric sequence. - $\sum _ { i = 1 } ^ { 8 } \left( \frac { 4 } { 3 } \right) ^ { i }$

Use Summation Notation - $\sum _ { \mathrm { i } = 1 } ^ { 5 } \frac { ( \mathrm { i } - 1 ) ! } { ( \mathrm { i } + 2 ) ! }$

A statement Sn about the positive integers is given. Write statements S1, S2, and S3, and show that each of these statements is true. - $S _ { n } : 3 + 8 + 13 + \ldots + ( 5 n - 2 ) = \frac { n ( 5 n + 1 ) } { 2 }$

Write the first four terms of the sequence whose general term is given. - $a _ { n } = \left( \frac { 1 } { 3 } \right) ^ { n }$

Use the Combinations Formula -8C0

Write a formula for the general term (the nth term) of the geometric sequence. - $2,6,18,54,162 , \ldots$

Write the first four terms of the sequence whose general term is given. - $a _ { n } = 2 n$

Use Summation Notation - $\sum _ { i = 1 } ^ { 4 } 2 ^ { i }$

Expand a Binomial Raised to a Power - $\left( x ^ { 2 } + 4 y \right) ^ { 4 }$

Evaluate the given binomial coefficient. - $\left( \begin{array} { l } 7 \\ 1 \end{array} \right)$

Use Recursion Formulas - $a _ { 1 } = 3$ and $a _ { n } = a _ { n - 1 } - 5$ for $n \geq 2$

Expand a Binomial Raised to a Power - $( 5 x - 4 y ) ^ { 3 }$

Write the first four terms of the sequence whose general term is given. -A deposit of $\$ 8000$ is made in an account that earns $8 \%$ interest compounded quarterly. The balance in the account after $n$ quarters is given by the sequence $a _ { n } = 8000 \left( 1 + \frac { 0.08 } { 4 } \right) ^ { n } \quad n = 1,2,3 , \ldots$ Find the balance in the account after 28 quarters.

Compute Theoretical Probability -Two 6-sided dice are rolled. What is the probability that the sum of the two numbers on the dice will be greater than 9?

Find the Value of an Annuity -Kurt deposits $150 each month into an account paying annual interest of 6% compounded monthly. How much will his account have in it at the end of 9 years?

Use Summation Notation - $\sum _ { i = 9 } ^ { 12 } \frac { 1 } { i - 3 }$

Evaluate the given binomial coefficient. - $\left( \begin{array} { l } 140 \\ 138 \end{array} \right)$