Exam 11: Sequences, Induction, and Probability

Express the sum using summation notation. Use a lower limit of summation not necessarily 1 and k for the index of summation. - $\frac { 3 } { 4 } + \frac { 4 } { 5 } + \frac { 5 } { 6 } + \frac { 6 } { 7 } + \ldots + \frac { 17 } { 18 }$

Compute Theoretical Probability -A lottery game contains 24 balls numbered 1 through 24 . What is the probability of choosing a ball numbered 25?

Write the word or phrase that best completes each statement or answers the question. Use mathematical induction to prove that the statement is true for every positive integer n. - $1 \cdot 8 + 2 \cdot 8 + 3 \cdot 8 + \ldots + 8 n = \frac { 8 n ( n + 1 ) } { 2 }$

Write the first four terms of the sequence whose general term is given. - $a _ { n } = ( - 1 ) ^ { n } ( n + 5 )$

Express the repeating decimal as a fraction in lowest terms. - $0 . \overline { 88 } = \frac { 88 } { 100 } + \frac { 88 } { 10,000 } + \frac { 88 } { 1,000,000 } + \ldots$

The general term of a sequence is given. Determine whether the given sequence is arithmetic, geometric, or neither. If the sequence is arithmetic, find the common difference; if it is geometric, find the common ratio. - $a _ { n } = 3 n ^ { 2 } - 4$

Find the Probability of One Event or a Second Event Occurring -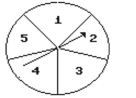 What is the probability that the arrow will land on 5 or 2 ?

The general term of a sequence is given. Determine whether the given sequence is arithmetic, geometric, or neither. If the sequence is arithmetic, find the common difference; if it is geometric, find the common ratio. - $a _ { n } = 2 n - 4$

Use the Formula for the Sum of an Infinite Geometric Series - $\sum _ { i = 1 } ^ { \infty } 10 ( - 0.2 ) ^ { \mathrm { i } - 1 }$

Write Terms of an Arithmetic Sequence - $\mathrm { a } _ { \mathrm { n } } = \mathrm { a } _ { \mathrm { n } } - 1 + \frac { 1 } { 3 } ; \mathrm { a } _ { 1 } = \frac { 4 } { 9 }$

Express the sum using summation notation. Use a lower limit of summation not necessarily 1 and k for the index of summation. -The finite sequence whose general term is $a _ { n } = 0.11 n ^ { 2 } - 1.06 n + 7.29$ where $n = 1,2,3 , \ldots , 9$ models the total operating costs, in millions of dollars, for a company from 1991 through $1999 .$ Find $\sum _ { \mathrm { i } = 1 } ^ { 5 } \mathrm { a } _ { \mathrm { i } }$

Write Terms of a Geometric Sequence - $a _ { n } = 5 a _ { n - 1 } ; a _ { 1 } = 4$

Express the sum using summation notation. Use a lower limit of summation not necessarily 1 and k for the index of summation. - $11 + 14 + 17 + 20 + \ldots + 35$

A statement Sn about the positive integers is given. Write statements S1, S2, and S3, and show that each of these statements is true. - $S _ { n } : 2 \text { is a factor of } n ^ { 2 } + 9 n$ 2 Prove Statements Using Mathematical Induction

The general term of a sequence is given. Determine whether the given sequence is arithmetic, geometric, or neither. If the sequence is arithmetic, find the common difference; if it is geometric, find the common ratio. -Ms. Patterson proposes to give her daughter Claire an allowance of $0.05 on the first day of her 14-day vacation, $0.10 on the second day, $0.20 on the third day, and so on. Find the allowance Claire would receive on the last day of her vacation.

Use Summation Notation - $\sum _ { i = 3 } ^ { 6 } ( 2 i - 2 )$

Express the sum using summation notation. Use 1 as the lower limit of summation and i for the index of summation. - $2 + 8 + 18 + \ldots + 50$

A statement Sn about the positive integers is given. Write statements S1, S2, and S3, and show that each of these statements is true. - $S _ { n } : 1 ^ { 2 } + 4 ^ { 2 } + 7 ^ { 2 } + \ldots + ( 3 n - 2 ) ^ { 2 } = \frac { n \left( 6 n ^ { 2 } - 3 n - 1 \right) } { 2 }$

Probability 1 Compute Empirical Probability -The table below represents the number of deaths per 100 cases for an illness having a median mortality of four years and a right-skewed distribution over time. What is the probability of living more than 12 years after diagnosis of the disease?

Write a formula for the general term (the nth term) of the arithmetic sequence. Then use the formula for $\mathbf { a } _ { \mathbf { n } }$ to find $a _ { 20 }$ , the 20th term of the sequence. - $\mathrm { a } _ { 1 } = - \frac { 4 } { 5 } , \mathrm {~d} = \frac { 2 } { 5 }$