Exam 11: Sequences, Induction, and Probability
Exam 1: Equations and Inequalities425 Questions
Exam 2: Functions and Graphs359 Questions
Exam 3: Polynomial and Rational Functions532 Questions
Exam 4: Exponential and Logarithmic Functions270 Questions
Exam 5: Trigonometric Functions386 Questions
Exam 6: Analytic Trigonometry226 Questions
Exam 7: Additional Topics in Trigonometry264 Questions
Exam 8: Systems of Equations and Inequalities288 Questions
Exam 9: Matrices and Determinants152 Questions
Exam 10: Conic Sections and Analytic Geometry228 Questions
Exam 11: Sequences, Induction, and Probability304 Questions
Exam 12: Prerequisites: Fundamental Concepts of Algebra409 Questions
Select questions type
Write the first four terms of the sequence whose general term is given.
-
(Multiple Choice)
5.0/5  (39)
(39)
Find the Probability of One Event or a Second Event Occurring
-Give the probability that the roll of a die will show 4 or 6 .
(Multiple Choice)
4.9/5  (38)
(38)
Use the Formula for the Sum of the First n Terms of an Arithmetic Sequence
-Find the sum of the first 30 terms of the arithmetic sequence: -13, -23, -33, -43, . . .
(Multiple Choice)
4.8/5  (34)
(34)
A statement Sn about the positive integers is given. Write statements S1, S2, and S3, and show that each of these
statements is true.
-
(Essay)
4.9/5  (39)
(39)
Use the Formula for the General Term of a Geometric Sequence
-Find when .
(Multiple Choice)
4.7/5  (44)
(44)
A statement Sn about the positive integers is given. Write statements S1, S2, and S3, and show that each of these
statements is true.
-
(Essay)
4.8/5  (38)
(38)
Find the Probability of One Event or a Second Event Occurring
-A card is drawn from a deck of 52 cards. What is the probability that it is a 6 or a diamond?
(Multiple Choice)
4.8/5  (39)
(39)
Use the Formula for the Sum of the First n Terms of an Arithmetic Sequence
-Find the sum of the odd integers between 142 and 72.
(Multiple Choice)
4.7/5  (42)
(42)
Find the Probability of One Event or a Second Event Occurring
-A spinner has regions numbered 1 through 15 . What is the probability that the spinner will stop on an even number or a multiple of 3 ?
(Multiple Choice)
4.8/5  (36)
(36)
Find the Probability of One Event and a Second Event Occurring
-A card is drawn from a well-shuffled deck of 52 cards. What is the probability that the card will have a value of 6 and be a face card?
(Multiple Choice)
4.9/5  (35)
(35)
Find the Value of an Annuity
-Looking ahead to retirement, you sign up for automatic savings in a fixed-income 401K plan that pays 5.5% per year compounded annually. You plan to invest $2000 at the end of each year for the next 25 years. How much will your account have in it at the end of 25 years?
(Multiple Choice)
4.7/5  (43)
(43)
Find the Probability of One Event or a Second Event Occurring
-What is the probability that the arrow will land on an odd number?
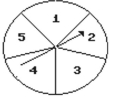
(Multiple Choice)
4.8/5  (37)
(37)
Express the sum using summation notation. Use a lower limit of summation not necessarily 1 and k for the index of summation.
-
(Multiple Choice)
4.7/5  (48)
(48)
Express the sum using summation notation. Use 1 as the lower limit of summation and i for the index of summation.
-
(Multiple Choice)
4.8/5  (40)
(40)
Use the formula for the sum of the first n terms of an arithmetic sequence to find the indicated sum.
-
(Multiple Choice)
4.8/5  (36)
(36)
Showing 261 - 280 of 304
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)