Exam 13: Simple Linear Regression

The Y-intercept (b0) represents the

SCENARIO 13-14-A You are the CEO of a dairy company. You are planning to expand production by purchasing additional cows, lands and hiring more workers. From the existing 50 farms owned by the company, you have collected data on total milk production (in liters) and the number of milking cows. The data are shown below and also available in the Excel file Scenario13-14-DataA.XLSX. MILK 84729 101969 103314 70574 76144 86695 87600 105272 120422 68749 85541 91910 110465 125369 159470 102930 113214 133328 140086 145514 152589 128304 138093 161368 208136 224205 231090 122204 132311 155154 177268 196449 205324 89562 94840 94997 97625 102226 103832 239673 239861 241298 249196 294455 318871 66483 100459 103847 154141 155516 COWS 18 24 22 19 21 19 22 19 24 18 20 25 26 27 29 24 25 28 26 28 27 21 24 27 33 32 32 22 25 26 29 29 28 25 21 23 24 28 25 39 40 40 39 42 47 19 20 21 25 31 You believe that the number of milking cows is the best predictor for total milk production on any given farm. -Referring to Scenario 13-14-A, the conclusion on the test of whether the number of milking cows is a good predictor for the total milk production using a 5% level of significance is

SCENARIO 13-8 It is believed that GPA (grade point average, based on a four point scale) should have a positive linear relationship with ACT scores. Given below is the Excel output for predicting GPA using ACT scores based a data set of 8 randomly chosen students from a Big-Ten university. Regressing GPA on ACT Regression Statistics Multiple R 0.7598 R Square 0.5774 Adjusted R Square 0.5069 Standard Error 0.2691 Observations 8 ANOVA df SS MS F Significance F Regression 1 0.5940 0.5940 8.1986 0.0286 Residual 6 0.4347 0.0724 Total 7 1.0287 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Intercept 0.5681 0.9284 0.6119 0.5630 -1.7036 2.8398 ACT 0.1021 0.0356 2.8633 0.0286 0.0148 0.1895 -Referring to Scenario 13-8, the interpretation of the coefficient of determination in this regression is

SCENARIO 13-10 The management of a chain electronic store would like to develop a model for predicting the weekly sales (in thousand of dollars) for individual stores based on the number of customers who made purchases. A random sample of 12 stores yields the following results: Customers Sales (Thousands of Dollars) 907 11.20 926 11.05 713 8.21 741 9.21 780 9.42 898 10.08 510 6.73 529 7.02 460 6.12 872 9.52 650 7.53 603 7.25 -Referring to Scenario 13-10, the value of the F test statistic equals the square of the t test statistic when testing whether the number of customers who make purchases is a good predictor for weekly sales.

EXPLANATION: The t-test statistic is $t = \frac { \left( b _ { 1 } - \beta _ { 1 } \right) } { S _ { b _ { 1 } } } = \frac { ( 2.5 - 3 ) } { 0.3536 } = - 1.4142$ KEYWORDS: t test on slope, p-value, slope SCENARIO 13-4 The managers of a brokerage firm are interested in finding out if the number of new clients a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new clients they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Scenario 13-4, the managers of the brokerage firm wanted to test the hypothesis that the number of new clients brought in did not affect the amount of sales generated. The value of the test statistic is _______.

SCENARIO 13-7 An investment specialist claims that if one holds a portfolio that moves in the opposite direction to the market index like the S&P 500, then it is possible to reduce the variability of the portfolio's return. In other words, one can create a portfolio with positive returns but less exposure to risk. A sample of 26 years of S&P 500 index and a portfolio consisting of stocks of private prisons, which are believed to be negatively related to the S&P 500 index, is collected. A regression analysis was performed by regressing the returns of the prison stocks portfolio (Y) on the returns of S&P 500 index (X) to prove that the prison stocks portfolio is negatively related to the S&P 500 index at a 5% level of significance. The results are given in the following EXCEL output. Coefficients \bullet Standard Error \bullet T Stat \bullet P- Coefficients Standard Error T Stat P-value Intercept 4.8660 0.3574 13.6136 0.0000 S\&P -0.5025 0.0716 -7.0186 0.0000 -Referring to Scenario 13-7, to test whether the prison stocks portfolio is negatively related to the S&P 500 index, the measured value of the test statistic is

EXPLANATION: The t-test statistic is $t = \frac { \left( b _ { 1 } - \beta _ { 1 } \right) } { S _ { b _ { 1 } } } = \frac { ( 2.5 - 3 ) } { 0.3536 } = - 1.4142$ KEYWORDS: t test on slope, p-value, slope SCENARIO 13-4 The managers of a brokerage firm are interested in finding out if the number of new clients a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new clients they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Scenario 13-4, ______% of the total variation in sales generated can be explained by the number of new clients brought in.

SCENARIO 13-3 The director of cooperative education at a state college wants to examine the effect of cooperative education job experience on marketability in the work place. She takes a random sample of 4 students. For these 4, she finds out how many times each had a cooperative education job and how many job offers they received upon graduation. These data are presented in the table below. Student CoopJobs JobOffer 1 1 4 2 2 6 3 1 3 4 0 1 -Referring to Scenario 13-3, the total sum of squares (SST) is __________.

SCENARIO 13-5 The managing partner of an advertising agency believes that his company's sales are related to the industry sales. He uses Microsoft Excel to analyze the last 4 years of quarterly data with the following results: 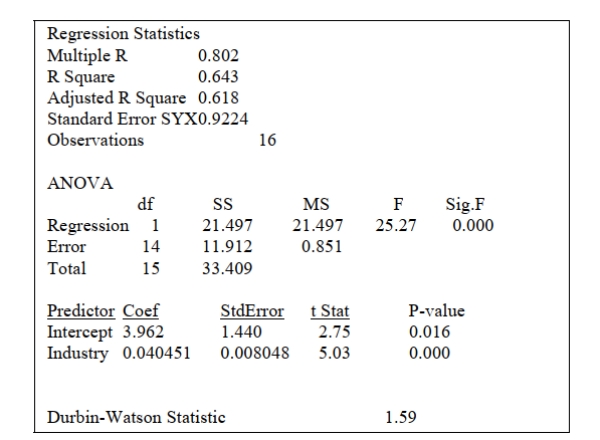-Referring to Scenario 13-5, the coefficient of determination is ________.

EXPLANATION: The t-test statistic is $t = \frac { \left( b _ { 1 } - \beta _ { 1 } \right) } { S _ { b _ { 1 } } } = \frac { ( 2.5 - 3 ) } { 0.3536 } = - 1.4142$ KEYWORDS: t test on slope, p-value, slope SCENARIO 13-4 The managers of a brokerage firm are interested in finding out if the number of new clients a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new clients they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Scenario 13-4, the regression sum of squares (SSR) is __________.

SCENARIO 13-5 The managing partner of an advertising agency believes that his company's sales are related to the industry sales. He uses Microsoft Excel to analyze the last 4 years of quarterly data with the following results: -Referring to Scenario 13-5, the prediction for a quarter in which X = 120 is Y = ________.

SCENARIO 13-1 A large national bank charges local companies for using their services. A bank official reported the results of a regression analysis designed to predict the bank's charges (Y) -- measured in dollars per month -- for services rendered to local companies. One independent variable used to predict service charges to a company is the company's sales revenue (X) -- measured in millions of dollars. Data for 21 companies who use the bank's services were used to fit the model: $Y _ { i } = \beta _ { 0 } + \beta _ { 1 } X _ { i } + \varepsilon _ { i }$ The results of the simple linear regression are provided below. $\hat { Y } = - 2,700 + 20 X , S _ { X X } = 65 , \text { two-tail } p \text { value } = 0.034 \left( \text { for testing } \beta _ { 1 } \right)$ -Referring to Scenario 13-1, interpret the estimate of $\beta _ { 0 }$ , the Y-intercept of the line.

SCENARIO 13-11 A computer software developer would like to use the number of downloads (in thousands) for the trial version of his new shareware to predict the amount of revenue (in thousands of dollars) he can make on the full version of the new shareware. 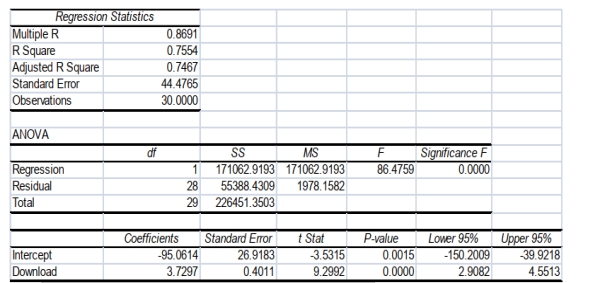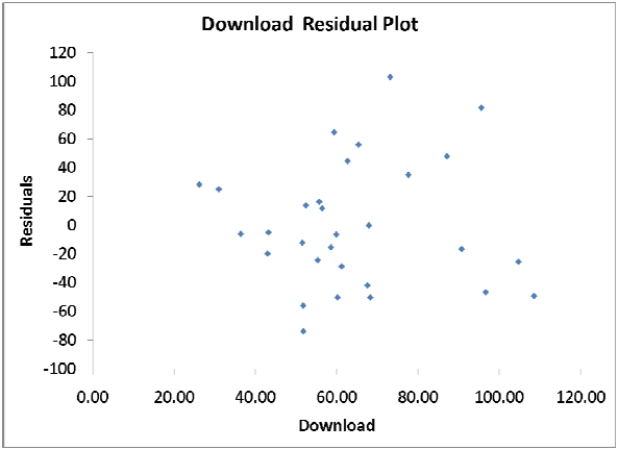Following is the output from a simple linear regression along with the residual plot and normal probability plot obtained from a data set of 30 different sharewares that he has developed: -Referring to Scenario 13-11, what is the critical value for testing whether there is a linear relationship between revenue and the number of downloads at a 5% level of significance?

The strength of the linear relationship between two numerical variables may be measured by the

EXPLANATION: The t-test statistic is $t = \frac { \left( b _ { 1 } - \beta _ { 1 } \right) } { S _ { b _ { 1 } } } = \frac { ( 2.5 - 3 ) } { 0.3536 } = - 1.4142$ KEYWORDS: t test on slope, p-value, slope SCENARIO 13-4 The managers of a brokerage firm are interested in finding out if the number of new clients a broker brings into the firm affects the sales generated by the broker. They sample 12 brokers and determine the number of new clients they have enrolled in the last year and their sales amounts in thousands of dollars. These data are presented in the table that follows. 1 27 52 2 11 37 3 42 64 4 33 55 5 15 29 6 15 34 7 25 58 8 36 59 9 28 44 10 30 48 11 17 31 12 22 38 -Referring to Scenario 13-4, set up a scatter plot.

A zero population correlation coefficient between a pair of random variables means that there is no linear relationship between the random variables.

SCENARIO 13-14-A You are the CEO of a dairy company. You are planning to expand production by purchasing additional cows, lands and hiring more workers. From the existing 50 farms owned by the company, you have collected data on total milk production (in liters) and the number of milking cows. The data are shown below and also available in the Excel file Scenario13-14-DataA.XLSX. MILK 84729 101969 103314 70574 76144 86695 87600 105272 120422 68749 85541 91910 110465 125369 159470 102930 113214 133328 140086 145514 152589 128304 138093 161368 208136 224205 231090 122204 132311 155154 177268 196449 205324 89562 94840 94997 97625 102226 103832 239673 239861 241298 249196 294455 318871 66483 100459 103847 154141 155516 COWS 18 24 22 19 21 19 22 19 24 18 20 25 26 27 29 24 25 28 26 28 27 21 24 27 33 32 32 22 25 26 29 29 28 25 21 23 24 28 25 39 40 40 39 42 47 19 20 21 25 31 You believe that the number of milking cows is the best predictor for total milk production on any given farm. -Referring to Scenario 13-14-A, if you purchase 40 cows for the new farm, the lower and upper limit of the 95% confidence interval for the mean total milk production are _____ liters and _____ liters, respectively.

The Chancellor of a university has commissioned a team to collect data on students' GPAs and the amount of time they spend bar hopping every week (measured in minutes). He wants to know if imposing much tougher regulations on all campus bars to make it more difficult for students to spend time in any campus bar will have a significant impact on general students' GPAs. His team should use a t test on the slope of the population regression.

SCENARIO 13-13 In this era of tough economic conditions, voters increasingly ask the question: "Is the educational achievement level of students dependent on the amount of money the state in which they reside spends on education?" The partial computer output below is the result of using spending per student ($) as the independent variable and composite score which is the sum of the math, science and reading scores as the dependent variable on 35 states that participated in a study. The table includes only partial results. Regression Statistics Multiple R 0.3122 R Square 0.0975 Adjusted R 0.0701 Square Standard 26.9122 Error Observations 35 $\text { ANOVA }$ -Referring to Scenario 13-13, the decision on the test of whether composite score depends linearly on spending per student using a 10% level of significance is to ________ (reject or not reject) $H _ { 0 }$ .

If you wanted to find out if alcohol consumption (measured in fluid oz.) and grade point average on a 4-point scale are linearly related, you would perform a a. $\chi ^ { 2 }$ test for the difference in two proportions. b. $\chi ^ { 2 }$ test for independence. c. a $\mathrm { Z }$ test for the difference in two proportions. d. a $t$ test for a correlation coefficient.