Exam 8: Inferences Based on a Single Sample: Tests of Hypothesis
Exam 1: Statistics, Data, and Statistical Thinking73 Questions
Exam 2: Methods for Describing Sets of Data194 Questions
Exam 3: Probability283 Questions
Exam 4: Discrete Random Variables133 Questions
Exam 5: Continuous Random Variables139 Questions
Exam 6: Sampling Distributions47 Questions
Exam 7: Inferences Based on a Single Sample: Estimation With Confidence Intervals124 Questions
Exam 8: Inferences Based on a Single Sample: Tests of Hypothesis140 Questions
Exam 9: Inferences Based on a Two Samples: Confidence Intervals and Tests of Hypotheses94 Questions
Exam 10: Analysis of Variance: Comparing More Than Two Means90 Questions
Exam 11: Simple Linear Regression111 Questions
Exam 12: Multiple Regression and Model Building131 Questions
Exam 13: Categorical Data Analysis60 Questions
Exam 14: Nonparametric Statistics90 Questions
Select questions type
Type I errors and Type II errors are complementary events so that α = P(Type I error) = 1 - P(Type II error) = 1 - β.
(True/False)
4.8/5  (40)
(40)
For the given rejection region, sketch the sampling distribution for z and indicate the location of the rejection region.
-z < -2.05 or z > 2.05
(Essay)
4.7/5  (31)
(31)
A large university is interested in learning about the average time it takes students to drive to campus. The university sampled 238 students and asked each to provide the amount of time they spent traveling to campus. This variable, travel time, was then used conduct a test of hypothesis. The goal was to determine if the average travel time of all the university's students differed from 20 minutes. Suppose the large-sample test statistic was calculated to be z = 2.14. Find the p-value for this test of hypothesis.
(Multiple Choice)
4.8/5  (29)
(29)
A company claims that 9 out of 10 doctors (i.e., 90%) recommend its brand of cough syrup to their patients. To test this claim against the alternative that the actual proportion is less than 90%, a random sample of doctors was taken. Suppose the test statistic is z = -2.23. Can we conclude that H0 should be rejected at the a) α = .10, b) α = .05, and c) α = .01 level?
(Multiple Choice)
4.8/5  (39)
(39)
The business college computing center wants to determine the proportion of business students who have laptop computers. If the proportion exceeds 35%, then the lab will scale back a proposed enlargement of its facilities. Suppose 300 business students were randomly sampled and 85 have laptops. Find the rejection region for the corresponding test using α = .10.
(Multiple Choice)
4.7/5  (35)
(35)
A new apparatus has been devised to replace the needle in administering vaccines. The apparatus, which is connected to a large supply of vaccine, can be set to inject different amounts of the serum, but the variance in the amount of serum injected to a given person must not be greater than .05 to ensure proper inoculation. A random sample of 31 injections resulted in a variance of .103. Specify the rejection region for the test. Use α = .10.
(Essay)
4.8/5  (30)
(30)
It has been estimated that the G-car obtains a mean of 40 miles per gallon on the highway, and the company that manufactures the car claims that it exceeds this estimate in highway driving. To support its assertion, the company randomly selects 64 G-cars and records the mileage obtained for each car over a driving course similar to that used to obtain the estimate. The following data resulted: x = 41.5 miles per gallon, s = 8 miles per gallon. Calculate the value of β if the true value of the mean is 42 miles per gallon. Use α = .025. 2 Find and Interpret Power of Test
(Essay)
4.7/5  (37)
(37)
An educational testing service designed an achievement test so that the range in student scores would be greater than 300 points. To determine whether the objective was achieved, the testing service gave the test to a random sample of 41 students and found that the sample mean and variance were 687 and 2605, respectively. Specify the null and alternative hypotheses for determining whether the test achieved the desired dispersion in scores. Assume that range = 6σ.
(Essay)
4.9/5  (32)
(32)
What is the probability associated with not making a Type II error? A)
B)
C)
D)
(Short Answer)
4.8/5  (38)
(38)
A random sample of n = 18 observations is selected from a normal population to test H0: μ = 145 against Ha: μ ≠ 145 at α = .10. Specify the rejection region.
(Essay)
4.9/5  (45)
(45)
A sample of 6 measurements, randomly selected from a normally distributed population, resulted in the following summary statistics: = 9.1, s = 1.5. Test the null hypothesis that the mean of the population is 10 against the alternative hypothesis μ < 10. Use α = .05.
(Essay)
4.8/5  (32)
(32)
A supermarket sells rotisserie chicken at a fixed price per chicken rather than by the weight of the chicken. The store advertises that the average weight of their chickens is 4.6 pounds. A random sample of 30 of the store's chickens yielded the weights (in pounds) shown below. 4.4 4.7 4.6 4.4 4.5 4.3 4.6 4.5 4.6 4.9 4.6 4.8 4.3 4.4 4.7 4.5 4.2 4.3 4.1 4.0 4.5 4.6 4.2 4.4 4.7 4.8 5.0 4.2 4.1 4.5 Test whether the population mean weight of the chickens is less than 4.6 pounds. Use α = .05.
(Essay)
4.9/5  (29)
(29)
A recipe submitted to a magazine by one of its subscribers states that the mean baking time for a cheesecake is 55 minutes. A test kitchen preparing the recipe before it is published in the magazine makes the cheesecake 10 times at different times of the day in different ovens. The following baking times (in minutes) are observed. 54 55 58 59 59 60 61 61 62 65 Assume that the baking times belong to a normal population. Test the null hypothesis that the mean baking time is 55 minutes against the alternative hypothesis μ > 55. Use α = .05.
(Essay)
4.9/5  (26)
(26)
The owner of Get-A-Away Travel has recently surveyed a random sample of 480 customers to determine whether the mean age of the agency's customers is over 28. The appropriate hypotheses are H0: μ = 28, Ha: μ > 28. If he concludes the mean age is over 28 when it is not, he makes a __________ error. If he concludes the mean age is not over 28 when it is, he makes a __________ error.
(Multiple Choice)
4.9/5  (40)
(40)
A supermarket sells rotisserie chicken at a fixed price per chicken rather than by the weight of the chicken. The store advertises that the average weight of their chickens is 4.6 pounds. A random sample of 30 of the store's chickens yielded the weights (in pounds) shown below. 4.4 4.7 4.6 4.4 4.5 4.3 4.6 4.5 4.6 4.9 4.6 4.8 4.3 4.4 4.7 4.5 4.2 4.3 4.1 4.0 4.5 4.6 4.2 4.4 4.7 4.8 5.0 4.2 4.1 4.5 Find and interpret the p-value in a test of H0: μ = 4.6 against Ha: μ < 4.6.
(Essay)
4.8/5  (34)
(34)
Based on the information in the screen below, what would you conclude in the test of H0: μ ≤ 14, Ha: μ > 14. Use α = .01. 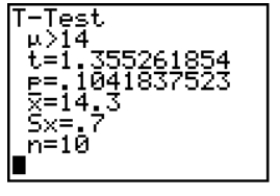
(Essay)
4.9/5  (34)
(34)
A large university is interested in learning about the average time it takes students to drive to campus. The university sampled 51 students and asked each to provide the amount of time they spent traveling to campus. The sample results found that the sample mean was 23.243 minutes and the sample standard deviation was 20.40 minutes. Find the rejection region for determining if the population standard deviation exceeds 20 minutes. Use α = 0.05. A) Reject if
B) Reject if
C) Reject if
D) Reject if 2 Perform Test of Hypothesis for Population Variance
(Short Answer)
4.8/5  (38)
(38)
A random sample of observations, selected from a normal population, is used to test the null hypothesis : . Specify the appropriate rejection region.
A)
B)
C)
D)
(Short Answer)
4.9/5  (42)
(42)
A consumer product magazine recently ran a story concerning the increasing prices of digital cameras. The story stated that digital camera prices dipped a couple of years ago, but now are beginning to increase in price because of added features. According to the story, the average price of all digital cameras a couple of years ago was $215.00. A random sample of n = 200 cameras was recently taken and entered into a spreadsheet. It was desired to test to determine if that average price of all digital cameras is now more than $215.00. Find the large-sample rejection region appropriate for this test if we are using α = 0.05. A) Reject if or .
B) Reject if or .
C) Reject if .
D) Reject if .
(Short Answer)
4.8/5  (30)
(30)
A national organization has been working with utilities throtughout the nation to find sites for large wind machines that generate electricity. Wind speeds must average more than 12 miles per hour (mph) for a site to be acceptable. Recently, the organization conducted wind speed tests at a particular site. Based on a sample of wind speed recordings (taken at random intervals), the wind speed at the site averaged mph, with a standard deviation of . To determine whether the site meets the organization's requirements, consider the test, vs. , where is the true mean wind speed at the site and . Fill in the blanks. "A Type I error in the context of this problem is to conclude that the true mean wind speed at the site 12 mph when it actually 12 mph."
A) exceeds; equals
B) equals; exceeds
C) equals; equals
D) exceeds; exceeds
(Short Answer)
4.8/5  (34)
(34)
Showing 41 - 60 of 140
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)