Exam 8: Inferences Based on a Single Sample: Tests of Hypothesis
Exam 1: Statistics, Data, and Statistical Thinking73 Questions
Exam 2: Methods for Describing Sets of Data194 Questions
Exam 3: Probability283 Questions
Exam 4: Discrete Random Variables133 Questions
Exam 5: Continuous Random Variables139 Questions
Exam 6: Sampling Distributions47 Questions
Exam 7: Inferences Based on a Single Sample: Estimation With Confidence Intervals124 Questions
Exam 8: Inferences Based on a Single Sample: Tests of Hypothesis140 Questions
Exam 9: Inferences Based on a Two Samples: Confidence Intervals and Tests of Hypotheses94 Questions
Exam 10: Analysis of Variance: Comparing More Than Two Means90 Questions
Exam 11: Simple Linear Regression111 Questions
Exam 12: Multiple Regression and Model Building131 Questions
Exam 13: Categorical Data Analysis60 Questions
Exam 14: Nonparametric Statistics90 Questions
Select questions type
A random sample of n = 15 observations is selected from a normal population to test H0: μ = 2.89 against Ha: μ < 2.89 at α = .01. Specify the rejection region.
(Essay)
4.9/5  (39)
(39)
A consumer product magazine recently ran a story concerning the increasing prices of digital cameras. The story stated that digital camera prices dipped a couple of years ago, but now are beginning to increase in price because of added features. According to the story, the average price of all digital cameras a couple of years ago was $215.00. A random sample of cameras was recently taken and entered into a spreadsheet. It was desired to test to determine if that average price of all digital cameras is now more than $215.00. The information was entered into a spreadsheet and the following printout was obtained: One-Sample T Test
Null Hypothesis:
Alternative Hyp:
Cases Included 22 Use the p- value given above to determine which of the following conclusions is correct.
(Multiple Choice)
4.9/5  (26)
(26)
Data were collected from the sale of 25 properties by a local real estate agent. The following printout concentrated on the land value variable from the sampled properties. HYPOTHESIS: MEAN X = x X = land_value SAMPLE MEAN OF X = 51,288 SAMPLE VARIANCE OF X = 273,643,254 SAMPLE SIZE OF X = 25 x = 46,845 MEAN X - x = 4443 t = 1.34293 D.F. = 24 P-VALUE = 0.1918585 P-VALUE/2 = 0.0959288 SD. ERROR = 3308.43 Suppose we are interested in testing whether the mean land value from this neighborhood differs from 46,845. Which hypotheses would you test? A) vs.
B) vs.
C) vs.
D) vs.
(Short Answer)
4.9/5  (38)
(38)
A rejection region is established in each tail of the sampling distribution for a two-tailed test.
(True/False)
4.9/5  (41)
(41)
A local eat-in pizza restaurant wants to investigate the possibility of starting to deliver pizzas. The owner of the store has determined that home delivery will be successful only if the average time spent on a delivery does not exceed 35 minutes. The owner has randomly selected 24 customers and delivered pizzas to their homes in order to test whether the mean delivery time actually exceeds 35 minutes. Suppose the p-value for the test was found to be .0274. State the correct conclusion.
(Multiple Choice)
5.0/5  (39)
(39)
Identify the observed level of significance for the test summarized on the screen below and interpret its value. 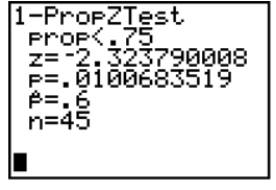 8.7 Calculating Type II Error Probabilities: More about β (Optional) 1 Find and Interpret β
8.7 Calculating Type II Error Probabilities: More about β (Optional) 1 Find and Interpret β
(Essay)
4.8/5  (35)
(35)
For the given rejection region, sketch the sampling distribution for z and indicate the location of the rejection region.
-z < -1.96
(Essay)
4.8/5  (30)
(30)
Researchers have claimed that the average number of headaches per student during a semester of Statistics is 10. Statistics students believe the average is higher. In a sample of n = 24 students the mean is 15 headaches with a deviation of 2. Which of the following represent the null and alternative hypotheses necessary to test the students' belief? A) vs.
B) vs.
C) vs.
D) vs.
(Short Answer)
4.8/5  (35)
(35)
Consider a test of . For the following case, give the rejection region for the test in terms of the z-statistic:
A)
B)
C)
D)
(Short Answer)
4.9/5  (36)
(36)
A national organization has been working with utilities throughout the nation to find sites for large wind machines that generate electricity. Wind speeds must average more than 16 miles per hour (mph) for a site to be acceptable. Recently, the organization conducted wind speed tests at a particular site. Based on a sample of n = 50 wind speed recordings (taken at random intervals), the wind speed at the site averaged x = 16.7 mph, with a standard deviation of s = 3.6 mph. To determine whether the site meets the organization's requirements, consider the test, H0: μ = 16 vs. Ha: μ > 16, where μ is the true mean wind speed at the site and α = .01. Suppose the value of the test statistic were computed to be 1.37. State the conclusion.
(Multiple Choice)
4.7/5  (37)
(37)
The business college computing center wants to determine the proportion of business students who have laptop computers. If the proportion differs from 25%, then the lab will modify a proposed enlargement of its facilities. Suppose a hypothesis test is conducted and the test statistic is 2.4. Find the p-value for a two-tailed test of hypothesis.
(Multiple Choice)
4.8/5  (33)
(33)
Data were collected from the sale of 25 properties by a local real estate agent. The following printout concentrated on the land value variable from the sampled properties. HYPOTHESIS: MEAN X = x X = land_value SAMPLE MEAN OF X = 51,315 SAMPLE VARIANCE OF X = 273,643,254 SAMPLE SIZE OF X = 25 x = 46,872 MEAN X - x = 4443 t = 1.34293 D.F. = 24 P-VALUE = 0.1918585 P-VALUE/2 = 0.0959288 SD. ERROR = 3308.43 What is the correct conclusion when testing a greater-than alternative hypothesis at α = .01?
(Multiple Choice)
4.8/5  (34)
(34)
It is desired to test H0: μ = 50 against HA: μ ≠ 50 using α = 0.10. The population in question is uniformly distributed with a standard deviation of 15. A random sample of 49 will be drawn from this population. If μ is really equal to 48, what is the probability that the hypothesis test would lead the investigator to commit a Type II error?
(Multiple Choice)
4.8/5  (33)
(33)
A local eat-in pizza restaurant wants to investigate the possibility of starting to deliver pizzas. The owner of the store has determined that home delivery will be successful only if the average time spent on a delivery does not exceed 34 minutes. The owner has randomly selected 19 customers and delivered pizzas to their homes. What hypotheses should the owner test to demonstrate that the pizza delivery will not be successful? A) vs.
B) vs.
C) vs.
D) vs.
(Short Answer)
4.8/5  (38)
(38)
A consumer product magazine recently ran a story concerning the increasing prices of digital cameras. The story stated that digital camera prices dipped a couple of years ago, but now are beginning to increase in price because of added features. According to the story, the average price of all digital cameras a couple of years ago was $215.00. A random sample of n = 22 cameras was recently taken and entered into a spreadsheet. It was desired to test to determine if that average price of all digital cameras is now more than $215.00. Find a rejection region appropriate for this test if we are using α = 0.05.
(Multiple Choice)
4.8/5  (37)
(37)
A small private college is interested in determining the percentage of its students who live off campus and drive to class. Specifically, it was desired to determine if less than 20% of their current students live off campus and drive to class. A sample of 108 students was randomly selected and the following printout was obtained: Hypothesis Test - One Proportion
Sample Size 108 Successes 16 Proportion 0.14815
Null Hypothesis:
Alternative Hyp:
Difference
Standard Error
-1.35 -value 0.0885 Based on the information contained in the printout, what conclusion would be correct when testing at α = 0.05. A) Reject
B) Fail to reject
C) Accept
D) Accept
(Short Answer)
4.7/5  (35)
(35)
It is desired to test H0: μ = 50 against HA: μ ≠ 50 using α = 0.10. The population in question is uniformly distributed with a standard deviation of 15. A random sample of 49 will be drawn from this population. If μ is really equal to 45, what is the power of the test?
(Multiple Choice)
4.9/5  (28)
(28)
A random sample of 100 observations is selected from a binomial population with unknown probability of success, p. The computed value of p^ is equal to .56. Find the observed levels of significance in a test of H0: = .5 against Ha: p > .5. Interpret the result.
(Essay)
4.7/5  (28)
(28)
Based on the information in the screen below, what would you conclude in the test of H0: μ ≤ 14, Ha: μ > 14. Use α = .01. 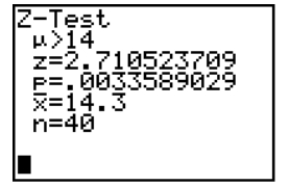
(Essay)
4.8/5  (37)
(37)
We never conclude "Accept " in a test of hypothesis. This is because:
A) (Type II error) is not known.
B) (Type I error) is not known.
C) is never true.
D) We want to be false.
(Short Answer)
4.9/5  (27)
(27)
Showing 81 - 100 of 140
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)