Exam 6: Systems and Matrices
Exam 1: Review of Basic Concepts637 Questions
Exam 2: Equations and Inequalities498 Questions
Exam 3: Graphs and Functions531 Questions
Exam 4: Polynomials and Rational Functions517 Questions
Exam 5: Inverse, Exponential, and Logarithmic Functions472 Questions
Exam 6: Systems and Matrices505 Questions
Exam 7: Arithmetic Sequence: Common Difference and First n Terms570 Questions
Select questions type
Solve the system by using the inverse of the coefficient matrix.
- 2x+8y+6z=20 4x+2y-2z=-2 3x-y+z=11
(Multiple Choice)
4.9/5  (37)
(37)
The graph shows the region of feasible solutions. Find the maximum or minimum value, as specified, of the objective
function.
-
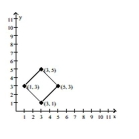
(Multiple Choice)
4.9/5  (38)
(38)
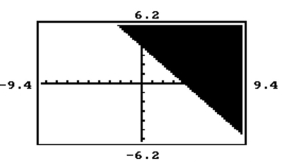
Determine the inequality which matches the calculator graph. Do not use your calculator. Instead, use your knowledge of
the concepts involved in graphing inequalities.
-
(Multiple Choice)
4.9/5  (30)
(30)
Choose the one alternative that best completes the statement or answers the question.
Graph the inequality.
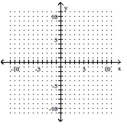
(Multiple Choice)
4.8/5  (40)
(40)
Choose the one alternative that best completes the statement or answers the question.
Graph the inequality.
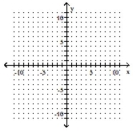
(Multiple Choice)
4.9/5  (35)
(35)
Solve the system. If the system has infinitely many solutions, write the solution set with x arbitrary.
-
(Multiple Choice)
4.9/5  (34)
(34)
The following graph shows the populations of the metropolitan areas of City X and City Y over six years. 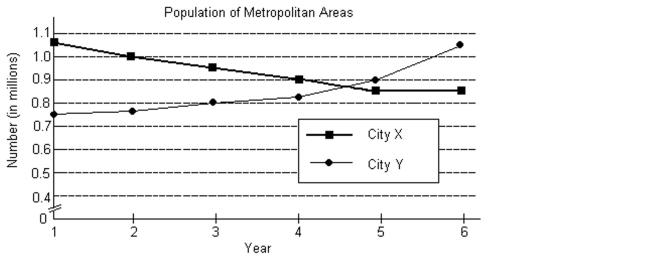 -Use the terms increasing, decreasing, and/or constant to describe the trends for the population of the City X metropolitan area.
-Use the terms increasing, decreasing, and/or constant to describe the trends for the population of the City X metropolitan area.
(Multiple Choice)
4.8/5  (33)
(33)
Use Cramer's rule to solve the system of equations. If D = 0, use another method to determine the solution set.
- x-3y=6 8x-2y=4
(Multiple Choice)
4.9/5  (35)
(35)
Find the partial fraction decomposition for the rational expression.
(Multiple Choice)
4.8/5  (39)
(39)
Provide an appropriate response.
-Describe the elements of a zero matrix.
(Multiple Choice)
4.7/5  (38)
(38)
Use the Gauss-Jordan method to solve the system of equations. If the system has infinitely many solutions, give the solution with y arbitrary.
- 4x+y=22 2x+5y=2
(Multiple Choice)
5.0/5  (31)
(31)
The following graph shows the populations of the metropolitan areas of City X and City Y over six years.  -Express the solution of the system as an ordered pair.
-Express the solution of the system as an ordered pair.
(Multiple Choice)
4.8/5  (28)
(28)
Graph the solution set of the system of inequalities.
- x+2y\geq2 x-y\leq0
(Multiple Choice)
4.9/5  (29)
(29)
Solve the system by using the inverse of the coefficient matrix.
-
(Multiple Choice)
4.7/5  (42)
(42)
A nonlinear system is given, along with the graphs of both equations in the system. Determine if the points of
intersection specified on the graph are solutions of the system by substituting directly into both equations.
- =y-1 y=-2x+16
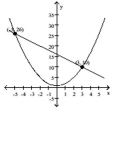
(Multiple Choice)
4.9/5  (32)
(32)
Find the partial fraction decomposition for the rational expression.
(Multiple Choice)
4.9/5  (32)
(32)
Use Cramer's rule to solve the system of equations. If D = 0, use another method to determine the solution set.
-3x-7y-6z=-65 5x+9y-5z=43 9x-9y+8z=95
(Multiple Choice)
4.8/5  (33)
(33)
Suppose that you are solving a system of three linear equations by the Gauss-Jordan method and obtain the following augmented matrix. What conclusion can you draw about the solutions of the system?
(Multiple Choice)
4.8/5  (41)
(41)
A nonlinear system is given, along with the graphs of both equations in the system. Determine if the points of
intersection specified on the graph are solutions of the system by substituting directly into both equations.
- +=25 2y+x=5
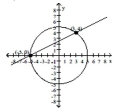
(Multiple Choice)
4.8/5  (32)
(32)
Showing 61 - 80 of 505
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)