Exam 8: Confidence Interval Estimation

True or False: The t distribution is used to develop a confidence interval estimate of the population proportion when the population standard deviation is unknown.

The t distribution

SCENARIO 8-7 A hotel chain wants to estimate the mean number of rooms rented daily in a given month. The population of rooms rented daily is assumed to be normally distributed for each month with a standard deviation of 240 rooms.During February, a sample of 25 days has a sample mean of 370 rooms. -True or False: Referring to Scenario 8-7, a 90% confidence interval calculated from the same data would be narrower than a 99% confidence interval.

True or False: The difference between the sample mean and the population mean is called the sampling error.

SCENARIO 8-8 The president of a university would like to estimate the proportion of the student population that owns a personal computer.In a sample of 500 students, 417 own a personal computer. -True or False: Referring to Scenario 8-8, it is possible that the 99% confidence interval calculated from the data will not contain the proportion of the student population who own a personal computer.

SCENARIO 8-5 A sample of salary offers (in thousands of dollars)given to management majors is: 48, 51, 46, 52, 47, 48, 47, 50, 51, and 59.Using this data to obtain a 95% confidence interval resulted in an interval from 47.19 to 52.61. -True or False: Referring to Scenario 8-5, a 99% confidence interval for the mean of the population from the same sample would be wider than 47.19 to 52.61.

SCENARIO 8-11 A poll was conducted by the marketing department of a video game company to determine the popularity of a new game that was targeted to be launched in three months.Telephone interviews with 1,500 young adults were conducted which revealed that 49% said they would purchase the new game.The margin of error was 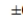3 percentage points. -Referring to Scenario 8-11, what is the needed sample size to obtain a 95% confidence interval in estimating the percentage of the targeted young adults who will purchase the new game to within 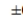5%?

True or False: The confidence interval obtained will always correctly estimate the population parameter.

True or False: Given a sample mean of 2.1 and a population standard deviation of 0.7 from a sample of 10 data points, a 90% confidence interval will have a width of 2.36.

A confidence interval was used to estimate the proportion of statistics students who are Female.A random sample of 72 statistics students generated the following 90% confidence Interval: (0.438, 0.642).Using the information above, what total size sample would be Necessary if we wanted to estimate the true proportion to within ±0.08 using 95% confidence?

True or False: The sample mean is a point estimate of the population mean.

True or False: The t distribution is used to construct confidence intervals for the population mean when the population standard deviation is unknown.

True or False: Other things being equal, the confidence interval for the mean will be wider for 95% confidence than for 90% confidence.

SCENARIO 8-4 The actual voltages of power packs labeled as 12 volts are as follows: 11.77, 11.90, 11.64, -True or False: Referring to Scenario 8-4, it is possible that the 99% confidence interval calculated from the data will not contain the mean voltage for the entire population.

True or False: The difference between the sample size and the population size is called the sampling error.

The t distribution approaches the standardized normal distribution when the number of degrees of freedom increases.

True or False: The standardized normal distribution is used to develop a confidence interval estimate of the population proportion when the sample size is sufficiently large.

SCENARIO 8-7 A hotel chain wants to estimate the mean number of rooms rented daily in a given month. The population of rooms rented daily is assumed to be normally distributed for each month with a standard deviation of 240 rooms.During February, a sample of 25 days has a sample mean of 370 rooms. -True or False: Referring to Scenario 8-7, the parameter of interest is the proportion of the rooms rented daily in a given month.