Exam 2: Graphs and Functions
Exam 1: Equations and Inequalities494 Questions
Exam 2: Graphs and Functions525 Questions
Exam 3: Polynomial and Rational Functions516 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions471 Questions
Exam 5: Trigonometric Functions301 Questions
Exam 6: The Circular Functions and Their Graphs289 Questions
Exam 7: Trigonometric Identities and Equations494 Questions
Exam 8: Applications of Trigonometry446 Questions
Exam 9: Systems and Matrices505 Questions
Exam 10: Analytic Geometry206 Questions
Exam 11: Further Topics in Algebra351 Questions
Exam 12: Review of Basic Concepts640 Questions
Select questions type
Describe the transformations and give the equation for the graph.
-
(Multiple Choice)
4.7/5  (36)
(36)
Solve the problem.
-A deep sea diving bell is being lowered at a constant rate. After 11 minutes, the bell is at a depth of 500 ft. After 40 minutes the bell is at a depth of 1800 ft. What is the average rate of change of
Depth? Round to one decimal place.
(Multiple Choice)
4.7/5  (36)
(36)
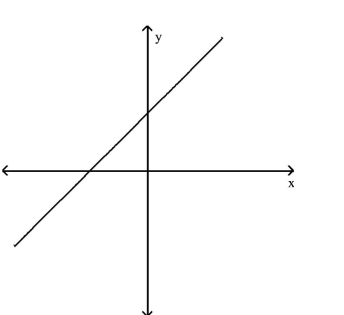
Choose the value which could represent the slope of the line. Assume that the scale on the x -axis is the same as the scale
on the y-axis.
-
(Multiple Choice)
4.9/5  (32)
(32)
Find the average rate of change illustrated in the graph.
-
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-The graph shows an idealized linear relationship for the average monthly payment to retirees from 1995 to 1999. Use the midpoint formula to estimate the average payment in 1997. Average Monthly Payment to Retirees

(Multiple Choice)
4.9/5  (41)
(41)
Solve the problem.
-The table lists how financial aid income cutoffs (in dollars) for a family of four have changed over time. Use the midpoint formula to approximate the financial aid cutoff for 1985. 
(Multiple Choice)
4.9/5  (42)
(42)
Evaluate.
-Find (f + g)(-3) when f(x) = x - 5 and g(x) = x + 3.
(Multiple Choice)
4.9/5  (43)
(43)
Solve the problem.
-Select the equation that describes the graph shown.
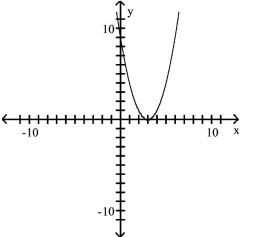
(Multiple Choice)
4.8/5  (44)
(44)
Determine whether the three points are collinear.
-(6, -2), (-2, 5), (1, 1)
(Multiple Choice)
4.8/5  (39)
(39)
Use a graphing calculator to solve the linear equation.
-The graph of is shown in the standard viewing window. Which is the only choice that could possibly be the solution of the equation ?
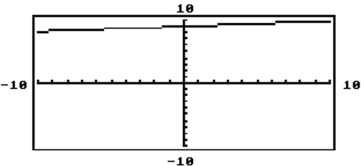
(Multiple Choice)
4.9/5  (34)
(34)
Consider the function h as defined. Find functions f and g so that (f ∘ g)(x) = h(x).
-
(Multiple Choice)
4.9/5  (48)
(48)
Showing 481 - 500 of 525
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)