Exam 30: Nuclear Physics and Radioactivity

How much energy is released when $0.60 \mu \mathrm { g }$ of $3 \mathrm { H }$ have decayed to $3 \mathrm { He }$ ? The mass of $3 \mathrm { He }$ is $3.0160293 \mathrm { u }$ , the mass of $3 \mathrm { H }$ is $3.0160492 \mathrm { u } , 1 \mathrm { u } = 931.5 \mathrm { MeV } / c ^ { 2 } , 1 \mathrm { eV } = 1.60 \times 10 ^ { - 19 } \mathrm {~J}$ , and $\mathrm { N } _ { \mathrm { A } } = 6.022 \times 10 ^ { 23 } \mathrm { molecules } / \mathrm { mol }$ .

The number of radioactive nuclei in a particular sample decreases to one-eighth of its original number in 9 days. What is the half-life of these nuclei?

Rubidium ${ } _ { 37 } ^ { 87 } \mathrm { Rb }$ is a naturally occurring isotope that undergoes $\beta ^ { - }$ decay. What isotope is the product of this decay?

A summary of the nuclear reactions that power our sun is $4 \mathrm { p } \rightarrow 4 \mathrm { He } + 2 \mathrm { e } ^ { - }$ , with masses of $938.272$ $\mathrm { MeV } / \mathrm { c } ^ { 2 }$ for a proton, $3727.38 \mathrm { MeV } / \mathrm { c } ^ { 2 }$ for the helium nucleus, and $0.511 \mathrm { MeV } / \mathrm { c } ^ { 2 }$ for each electron. How much energy is released by each of these reactions?

A radioactive isotope of atomic number $\mathrm { Z }$ emits an alpha particle, and the daughter nucleus then emits a beta-minus particle. What is the atomic number of the resulting nucleus?

A nuclear reaction is shown: ${ } _ { 5 } ^ { 10 } \mathrm {~B} + { } _ { 2 } ^ { 4 } \mathrm { He } \rightarrow { } _ { 1 } ^ { 1 } \mathrm { H } + ?$ . Which one of the following isotopes is the missing nuclear product?

A radioactive sample has a half-life of $10 \mathrm {~min}$ . What fraction of the sample is left after $40 \mathrm {~min}$ ?

Estimate the mass of a nucleus with radius $2.8 \times 10 ^ { - 15 } \mathrm {~m} . \left( 1 \mathrm { u } = 1.6605 \times 10 ^ { - 27 } \mathrm {~kg} \right)$

If the half-life of a material is 45 years, how much of it will be left after 100 years?

The neutral deuterium atom, ${ } _ { 1 } ^ { 2 } \mathrm { H }$ , has a mass of $2.014102 \mathrm { u }$ ; a neutral ordinary hydrogen atom has a mass of $1.007825 \mathrm { u }$ ; a neutron has a mass of $1.008665 \mathrm { u }$ ; and a proton has a mass of $1.007277 \mathrm { u }$ . What is the binding energy of the deuterium nucleus? $\left( 1 \mathrm { u } = 931.5 \mathrm { MeV } / \mathrm { c } ^ { 2 } \right)$

The radioactivity due to carbon-14 measured in a piece of a wooden casket from an ancient burial site is found to produce 20 counts per minute from a given sample, whereas the same amount of Carbon from a piece of living wood produces 160 counts per minute. The half-life of carbon-14, a Beta-minus emitter, is 5730 years. What would we calculate for the age of the artifact, assuming That the activity for living wood has remained constant over time?

Calculate the estimated nuclear radius of ${ } _ { 38 } ^ { 90 } \mathrm { Sr } ?$

Plutonium has a half life of $2.4 \times 10 ^ { 4 }$ years. How long does it take for $99.0 \%$ of the plutonium to decay?

A hospital patient has been given a sample of 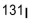, which has a half-life of $8.04$ days. This sample is decaying at $5.9$ times the acceptable level for exposure to the general public. How long must the patient wait for the decay rate of the sample to reach the acceptable level?

An old bone sample contains $321 \mathrm {~g}$ of carbon and has an activity of 947 decays/min due to the carbon-14 in it. The half-life of carbon-14 is $5730 \mathrm { y }$ . Assume that the activity of the atmospheric carbon is, and has remained, $0.255 \mathrm {~Bq}$ per gram of carbon. (a) How old is the sample? (b) What will be the activity of the sample $2000 \mathrm { y }$ from now, in decays per minute?

An excited ${ } _ { 92 } ^ { 236 } \mathrm { U } ^ { * }$ nucleus undergoes fission into two fragments as follows: ${ } _ { 92 } ^ { 236 } \mathrm { U } ^ { * } \rightarrow { } _ { 56 } ^ { 144 } \mathrm { Ba } + { } _ { 36 } ^ { 92 } \mathrm { Kr }$ If, at the instant of fission, the $\mathrm { Ba }$ and $\mathrm { Kr }$ fragments are spherical and just barely in contact, what is the electrostatic potential energy of these two fragments? ( $1 \mathrm { eV } = 1.60 \times 10 ^ { - 19 } \mathrm {~J} , e = 1.60 \times 10 ^ { - 19 } \mathrm { C }$ , $1 / 4 \pi \varepsilon _ { 0 } = 8.99 \times 10 ^ { 9 } \mathrm {~N} \cdot \mathrm { m } ^ { 2 } / \mathrm { C } ^ { 2 }$ )

A $\beta$ - particle is also known as

What happens to the half-life of a radioactive substance as we increase its temperature?

The following masses are known: 1.008665 1.007825 226.025403 What is the binding energy of ${ } _ { 88 } ^ { 226 } \mathrm { Ra }$ ? $\left( 1 \mathrm { u } = 931.5 \mathrm { MeV } / \mathrm { c } ^ { 2 } \right)$

A sample of wood has been recovered by an archaeologist. The sample is sent to a laboratory, where it is determined that the activity of the sample is 0.144 Bq/g. By comparing this activity with The activity of living organic matter, which is 0.230 Bq/g, the scientist determines how old the wood Sample is, or more precisely, when the tree that the sample came from died. Carbon-14 has a Half-life of 5730 years. If the activity of living matter has been constant over time, how old is the Sample of wood?