Exam 7: Applications of Trigonometry and Vectors

Solve the problem. -Tia is going to stain her triangular concrete patio. The patio is approximately 10 feet by 17 feet by 13 feet. If one can of stain covers $17 \mathrm { ft } ^ { 2 }$ , how many cans of stain will she need?

Find the missing parts of the triangle. -A = 20° a = 35 km B = 50 km If necessary, round angles to the nearest whole number and side lengths to the nearest km.

Solve the problem. -If $\mathbf { u } = \langle - 5,7 \rangle , \mathbf { v } = \langle - 1,6 \rangle$ , and $\mathbf { w } = \langle - 11,2 \rangle$ , evaluate $\mathbf { u } \cdot ( \mathbf { v } + \mathbf { w } )$

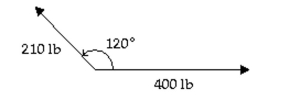
Use the parallelogram rule to find the magnitude of the resultant force for the two forces shown in the figure. Round to one decimal place. -

Find the indicated vector. -Let $\mathbf { u } = \langle 8 , - 5 \rangle , \mathbf { v } = \langle 2 , - 1 \rangle$ . Find $\mathbf { u } + \mathbf { v }$ .

Determine whether there is sufficient information for solving a triangle, with the given combination of angles and sides, by the law of sines. -B, a, and c

Sketch the vectors u and w with angle between them and sketch the resultant. - $| \mathbf { u } | = 5 , | \mathbf { w } | = 5 , \theta = 45 ^ { \circ }$

Solve the problem. -Two points A and B are on opposite sides of a building. A surveyor chooses a third point C 77 yd from B and 95 yd from A, with angle ACB measuring 54.3°. How far apart are A and B (to the Nearest yard)?

Solve the problem. -Two forces of 425 newtons and 267 newtons act at a point. The resultant force is 507 newtons. Find the angle between the forces.

Find the area of triangle ABC with the given parts. Round to the nearest tenth when necessary. -a = 46 ft b = 54 ft C = 62 ft

Solve the problem. -Starting at point A, a ship sails 48 km on a bearing of 217°, then turns and sails 15 km on a bearing of 280°. Find the distance of the ship from point A.

Graph the polar equation for in [0°, 360°). -Why can't the Pythagorean theorem be used to solve an oblique triangle?

Find the missing parts of the triangle. -A = 97.3° b = 15.2 ft A = 30.7 ft If necessary, round angles and side lengths to the nearest tenth.

Draw a sketch to represent the vector. Refer to the vectors pictured here. - $c + d$

Find the magnitude and direction angle (to the nearest tenth) for each vector. Give the measure of the direction angle as an angle in [0,360°]. - $\langle 10,10 \rangle$

Use the figure to find the specified vector. -Find a + b.

Solve the problem. -A guy wire to a tower makes a 67° angle with level ground. At a point 33 ft farther from the tower than the wire but on the same side of the base as the wire, the angle of elevation to the top of the Pole is 38°. Find the wire length (to the nearest foot).

Draw a sketch to represent the vector. Refer to the vectors pictured here. -b + c

Find the indicated vector. -Let $\mathbf { u } = \langle 1,8 \rangle , \mathbf { v } = \langle 9,6 \rangle$ . Find $\mathbf { v } - \mathbf { u }$ .

Solve the problem. -To find the distance AB across a river, a distance BC = 346 m is laid off on one side of the river. It is found that B = 115.1° and C = 13.6°. Find AB rounded to the nearest meter.