Exam 2: Acute Angles and Right Triangles
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Solve the problem.
-A 35-foot ladder is leaning against the side of a building. If the ladder makes an angle of 24° with the side of the building, how far is the bottom of the ladder from the base of the building?
Round your answer to the hundredths place when necessary.
Free
(Multiple Choice)
4.7/5  (36)
(36)
Correct Answer:
A
Solve the right triangle.
-A = 19° 17´, c = 287 ft, C = 90° Round side lengths to two decimal places, if necessary.
Free
(Multiple Choice)
4.9/5  (32)
(32)
Correct Answer:
D
Solve the problem.
-Find h as indicated in the figure. Round to the nearest foot. 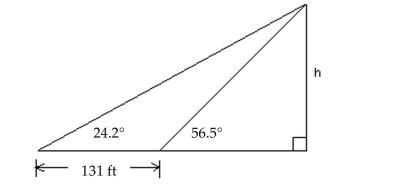
Free
(Multiple Choice)
4.7/5  (38)
(38)
Correct Answer:
B
Find all values of , if is in the interval [0, 360°) and has the given function value.
-
(Multiple Choice)
4.8/5  (33)
(33)
The number represents an approximate measurement. State the range represented by the measurement.
-24.35 k
(Multiple Choice)
5.0/5  (33)
(33)
Suppose ABC is a right triangle with sides of lengths a, b, and c and right angle at C. Find the unknown side length using
the Pythagorean theorem and then find the value of the indicated trigonometric function of the given angle. Rationalize
the denominator if applicable.
-Find when and .
(Multiple Choice)
4.8/5  (38)
(38)
Determine whether the statement is true or false.
-cos 60° = cos 180° - cos 120°
(True/False)
4.8/5  (33)
(33)
Solve the problem.
-From a boat on the lake, the angle of elevation to the top of a cliff is 13°11'. If the base of the cliff is 1683 feet from the boat, how high is the cliff (to the nearest foot)?
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-The grade resistance F of a car traveling up or down a hill is modeled by the equation F = W sin ϴ where W is the weight of the car and ϴ is the angle of the hill's grade (ϴ > 0 for uphill travel, ϴ < 0
For downhill travel). A 2025-lb car has just rolled off a sheer vertical cliff (ϴ = -90°). What is the
Car's grade resistance?
(Multiple Choice)
5.0/5  (34)
(34)
Suppose ABC is a right triangle with sides of lengths a, b, and c and right angle at C. Find the unknown side length using
the Pythagorean theorem and then find the value of the indicated trigonometric function of the given angle. Rationalize
the denominator if applicable.
-Find when and .
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-The grade resistance of a car traveling up or down a hill is modeled by the equation , where is the weight of the car and is the angle of the hill's grade for uphill travel, for downhill travel). Find the weight of the car (to the nearest pound) that is traveling on downhill grade and which has a grade resistance of .
(Multiple Choice)
4.8/5  (36)
(36)
Solve the right triangle.
-a = 2.6 in., A = 49.8°, C = 90° Round values to one decimal place.
(Multiple Choice)
4.9/5  (23)
(23)
Solve the problem.
-Find the exact value of x in the figure. 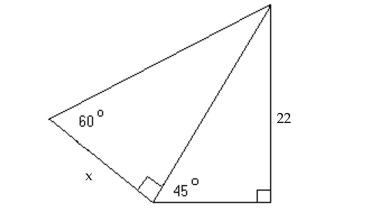
(Multiple Choice)
4.7/5  (33)
(33)
Decide whether the statement is true or false.
-tan 23° < tan 4°
(True/False)
4.9/5  (36)
(36)
Decide whether the statement is true or false.
-tan 28° > cot 28°
(True/False)
4.8/5  (35)
(35)
Write the function in terms of its cofunction. Assume that any angle in which an unknown appears is an acute angle.
-
(Multiple Choice)
4.8/5  (41)
(41)
Showing 1 - 20 of 204
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)