Exam 4: Graphs of the Circular Functions
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Match the function with its graph.
-1)
2)
3)
4)
a)
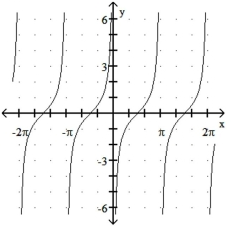 b)
b)
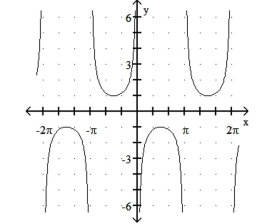 c)
c)
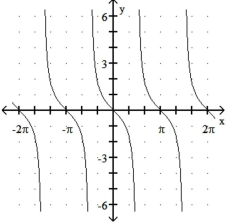 d)
d)
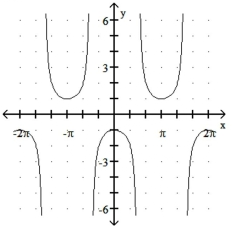
Free
(Multiple Choice)
4.9/5  (29)
(29)
Correct Answer:
D
Use Identities to find the exact value.
-Tides go up and down in a 14.8-hour period. The average depth of a certain river is 7 m and ranges from 4 to 10 m. The variation can be approximated by a sine curve. Write an equation that gives the
Approximate variation y, if x is the number of hours after midnight and high tide occurs at 5:00 am.
Free
(Multiple Choice)
4.7/5  (34)
(34)
Correct Answer:
A
Give the amplitude or period as requested.
-Period of y = sin 3x
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-The voltage E in an electrical circuit is given by E = 1.3 cos 100πt, where t is time measured in seconds. Find the period.
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem.
-A weight attached to a spring is pulled down 8 inches below the equilibrium position. Assuming that the frequency of the system is cycles per second, determine a trigonometric model that gives the position of the weight at time second.
(Multiple Choice)
4.8/5  (35)
(35)
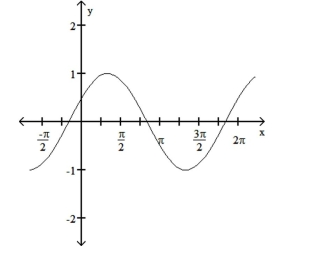
The function graphed is of the form y = cos x + c, y = sin x + c, y = cos(x - d), or y = sin(x - d), where d is the least possible
positive value. Determine the equation of the graph.
-
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-The temperature in Fairbanks is approximated by
where is the temperature on day , with corresponding to Jan. 1 and corresponding to Dec. 31. Estimate the temperature on day 49 .
(Multiple Choice)
4.7/5  (32)
(32)
Match the function with its graph.
-1)
2)
3)
4)
a)
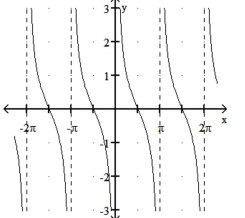 b)
b)
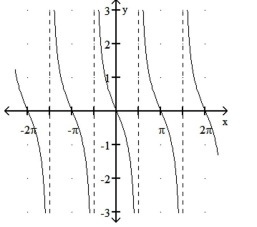 c)
c)
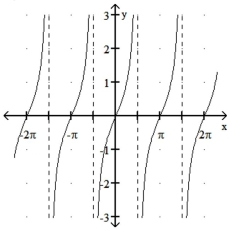 d)
d)
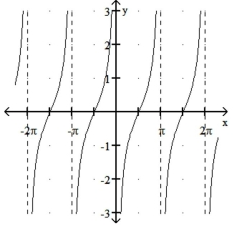
(Multiple Choice)
4.8/5  (27)
(27)
Showing 1 - 20 of 137
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)