Exam 3: Radian Measure and the Unit Circle
Exam 1: Trigonometric Functions188 Questions
Exam 2: Acute Angles and Right Triangles204 Questions
Exam 3: Radian Measure and the Unit Circle167 Questions
Exam 4: Graphs of the Circular Functions137 Questions
Exam 5: Trigonometric Identities321 Questions
Exam 6: Inverse Circular Functions and Trigonometric Equations179 Questions
Exam 7: Applications of Trigonometry and Vectors103 Questions
Exam 8: Complex Numbers, Polar Equations, and Parametric Equations60 Questions
Select questions type
Solve the problem.
-Suppose the tip of the minute hand of a clock is 5 in. from the center of the clock. Determine the distance traveled by the tip of the minute hand in hours. Give an exact answer.
(Multiple Choice)
4.7/5  (30)
(30)
Solve the problem.
-Let angle POQ be designated ϴ. Angles PQR and VRQ are right angles. If ϴ = 13°, find the length of US accurate to four decimal places. 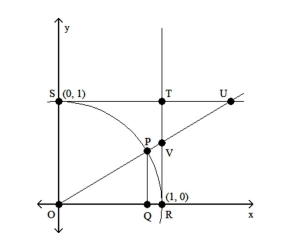
(Multiple Choice)
5.0/5  (34)
(34)
Convert the degree measure to radians. Leave answer as a multiple of
-
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-The minute hand of a clock is 13 inches long. What distance does its tip move in 16 minutes? Give an exact answer.
(Multiple Choice)
4.9/5  (35)
(35)
For the given value of s, decide in which quadrant an angle of s radians lies by evaluating sin s and cos s.
-s = 66
(Multiple Choice)
4.8/5  (36)
(36)
Suppose an arc of length lies on the unit circle , starting at point and terminating at the point ( , ). Use a calculator to find the approximate coordinates . Round coordinates to four decimal places when appropriate.
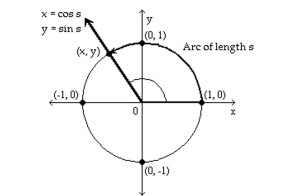 The unit circle
-s = 5.6
The unit circle
-s = 5.6
(Multiple Choice)
4.8/5  (30)
(30)
Find the length of an arc intercepted by a central angle in a circle of radius r. Round your answer to 1 decimal place.
-r = 115.19 in.; ϴ = 195°
(Multiple Choice)
4.7/5  (35)
(35)
Convert the radian measure to degrees. Round to the nearest hundredth if necessary.
-
(Multiple Choice)
4.8/5  (27)
(27)
Convert the degree measure to radians. Leave answer as a multiple of
--470°
(Multiple Choice)
4.8/5  (35)
(35)
The figure shows an angle in standard position with its terminal side intersecting the unit circle. Evaluate the indicated
circular function value of .
-
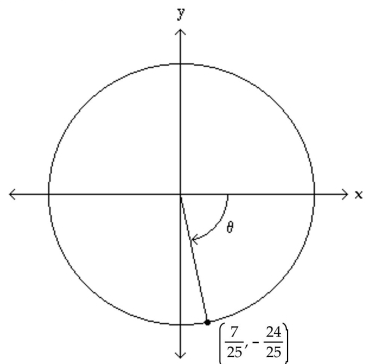
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-A wheel is rotating at 5 radians/sec, and the wheel has a 83-inch diameter. To the nearest foot, what is the speed of a point on the rim in ft/min?
(Multiple Choice)
4.9/5  (38)
(38)
Convert the degree measure to radians. Leave answer as a multiple of
--45°
(Multiple Choice)
4.8/5  (37)
(37)
Convert the radian measure to degrees. Round to the nearest hundredth if necessary.
-
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-A circular sector has an area of 18 in and an arc length of 3 inches. What is the measure of the central angle in degrees? Round to the nearest degree.
(Multiple Choice)
4.8/5  (24)
(24)
Solve the problem.
-The temperature in Verlander is modeled by where is the temperature in degrees Fahrenheit on day , with representing January 1 and representing December 31 . Find the temperature on July 7 .
(Multiple Choice)
4.8/5  (41)
(41)
Showing 61 - 80 of 167
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)