Exam 22: Multifactor Models
Exam 1: An Introduction to Fixed Income Markets17 Questions
Exam 2: Basics of Fixed Income Securities20 Questions
Exam 3: Basics of Interest Rate Risk Management17 Questions
Exam 4: Basic Refinements in Interest Rate Risk Management18 Questions
Exam 5: Interest Rate Derivatives: Forwards and Swaps15 Questions
Exam 6: Interest Rate Derivatives: Futures and Options15 Questions
Exam 7: Inflation, Monetary Policy, and the Federal Funds Rate15 Questions
Exam 8: Basics of Residential Mortgage Backed Securities21 Questions
Exam 9: One Step Binomial Trees15 Questions
Exam 10: Multi-Step Binomial Trees15 Questions
Exam 11: Risk Neutral Trees and Derivative Pricing18 Questions
Exam 12: American Options19 Questions
Exam 13: Monte Carlo Simulations on Trees18 Questions
Exam 14: Interest Rate Models in Continuous Time15 Questions
Exam 15: No Arbitrage and the Pricing of Interest Rate Securities17 Questions
Exam 16: Dynamic Hedging and Relative Value Trades13 Questions
Exam 17: Dynamic Hedging and Relative Value Trades18 Questions
Exam 18: The Risk and Return of Interest Rate Securities11 Questions
Exam 19: No Arbitrage Models and Standard Derivatives20 Questions
Exam 20: The Market Model for Standard Derivatives19 Questions
Exam 21: Forward Risk Neutral Pricing and the Libor Market Model14 Questions
Exam 22: Multifactor Models16 Questions
Select questions type
In the Vasicek one factor model, the short rate determines the model. In the Vasicek two factor model, what rates drive the model?
Free
(Essay)
4.8/5  (38)
(38)
Correct Answer:
In the two factor model it is the short rate and the long rate that determine the rest of the rate dynamics in the term structure.
Under the Vasicek model, what degree of correlation do different interest rates have?
Free
(Essay)
4.8/5  (35)
(35)
Correct Answer:
Rates on the term structure are perfectly correlated in the Vasicek model.
When are multifactor models used?
Free
(Essay)
4.8/5  (30)
(30)
Correct Answer:
When we want to allow independent variation in the level, slope and cur- vature components of the yield curve.
What is the difference between using a model for finding arbitrage oppor- tunities and using a model for pricing derivatives and other securities?
(Essay)
4.9/5  (40)
(40)
Can a solution always be found in order to price a security as proposed by the Feynman-Kac formula?
(Essay)
4.7/5  (36)
(36)
What peculiarity of a yield curve steepner makes the use of 2-factor models attractive?
(Essay)
4.9/5  (34)
(34)
What modi?cations should be included to Ito's lemma when we allow correlation between the two factors?
(Essay)
4.8/5  (31)
(31)
What advantages does the 2-factor Vasicek have when fitting volatility?
(Essay)
4.7/5  (44)
(44)
In the 2-factor Hull-White model, what is the benefit of introducing θt (time dependent central tendency)?
(Essay)
4.8/5  (40)
(40)
Why is it considered that implied volatility of interest rate options has a "hump" shape?
(Essay)
4.8/5  (41)
(41)
Given that we now have two stochastic factors, when writing Ito's lemma as the following 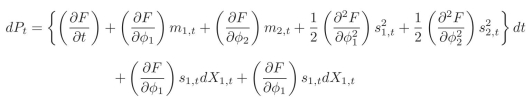 what are we implicitly assuming about them?
what are we implicitly assuming about them?
(Essay)
4.9/5  (38)
(38)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)