Exam 11: Analyzing Algorithm Efficiency
Exam 1: Speaking Mathematically13 Questions
Exam 2: The Logic of Compound Statements27 Questions
Exam 3: The Logic of Quantified Statements16 Questions
Exam 4: Elementary Number Theory and Methods of Proof28 Questions
Exam 5: Sequences, Mathematical Induction, and Recursion37 Questions
Exam 6: Set Theory19 Questions
Exam 7: Functions21 Questions
Exam 8: Relations19 Questions
Exam 9: Counting and Probability25 Questions
Exam 10: Graphs and Trees14 Questions
Exam 11: Analyzing Algorithm Efficiency22 Questions
Exam 12: Regular Expressions and Finite State Automata14 Questions
Select questions type
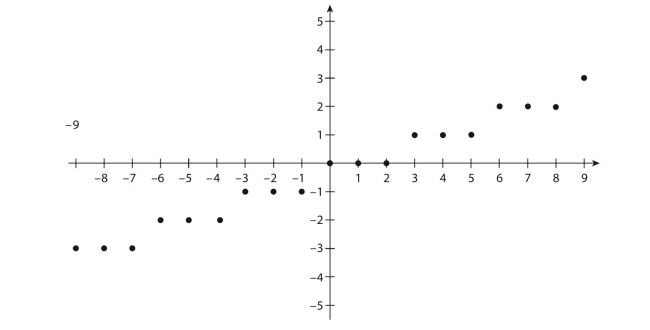
Draw a careful graph of the function f defined by the formula
for all integers n.
Free
(Essay)
4.9/5  (29)
(29)
Correct Answer:
(a) Consider the following algorithm segment:
for to
for to
next
next
How many additions and multiplications are performed when the inner loop of this algorithm segment is executed? How many additions and multiplications are performed when the entire algorithm segment is executed?
(b) Find an order for this algorithm segment from among the following: , , and . Give a reason for your answer.
Free
(Essay)
4.9/5  (42)
(42)
Correct Answer:
a. Two multiplications and one addition are performed when the inner loop of the given
algorithm segment is executed for a total of three elementary operations for each iteration of
the inner loop. The number of iterations of the inner loop can be deduced from the following
table, which shows the values of i and j for which the inner loop is executed.
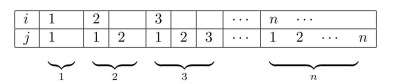
Therefore, by Theorem , the number of iterations of the inner loop is
The total number of elementary operations that must be performed when the algorithm is executed is the number performed during each iteration of the inner loop times the number of iterations of the inner loop:
b. By the theorem on polynomial orders, is , and so the algorithm segment has order .
Express the following statement using Ω-notation.:
Free
(Essay)
5.0/5  (36)
(36)
Correct Answer:
Explain why the following statement is true. (You may use the theorem on polynomial orders.)
(Essay)
4.8/5  (35)
(35)
If and are positive integers and , what is ? Be sure to justify each step of your answer.
(Essay)
4.7/5  (32)
(32)
Use the definition of -notation to prove that is . (Do not use the theorem on polynomial orders.)
(Essay)
4.9/5  (38)
(38)
Use the definition of -notation to prove that is .(Do not use the theorem on polynomial orders.)
(Essay)
5.0/5  (36)
(36)
Let h be the function whose graph is shown below. Carefully sketch the graph of 2h. 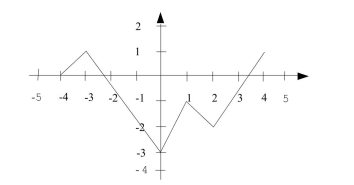
(Essay)
4.8/5  (37)
(37)
(a) Find the total number of additions and multiplications that must be performed when the following algorithm is executed. Show your work carefully.
(b) Find an order for the algorithm segment of part (a) from among the following: , , and . Give a reason for your answer.
(Essay)
4.9/5  (43)
(43)
Define a function by the formula for all positive real numbers .
(a) Graph , marking units carefully on your axes.
(b) What is ? Why?
(c) Write the equation in logarithmic form.
(Essay)
4.8/5  (34)
(34)
Showing 1 - 20 of 22
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)