Exam 7: The Cost of Being Connected
Exam 1: The Mathematics of Elections: the Paradoxes of Democracy40 Questions
Exam 2: The Mathematics of Power: Weighted Voting40 Questions
Exam 3: The Mathematics of Sharing: Fair-Division Games38 Questions
Exam 4: The Mathematics of Apportionment: Making the Rounds40 Questions
Exam 5: The Mathematics of Getting Around: Euler Paths and Circuits37 Questions
Exam 6: The Mathematics of Touring: Traveling Salesman Problems40 Questions
Exam 7: The Cost of Being Connected40 Questions
Exam 8: The Mathematics of Scheduling: Chasing the Critical Path40 Questions
Exam 9: Population Growth Models: There Is Strength in Numbers40 Questions
Exam 10: Financial Mathematics: Money Matters40 Questions
Exam 11: The Mathematics of Symmetry: Beyond Reflection40 Questions
Exam 12: Fractal Geometry: the Kinky Nature of Nature39 Questions
Exam 13: Fibonacci Numbers and the Golden Ratio: Tales of Rabbits and Gnomons40 Questions
Exam 14: Censuses, Surveys, Polls, and Studies: the Joys of Collecting Data40 Questions
Exam 15: Graphs, Charts, and Numbers: the Data Show and Tell40 Questions
Exam 16: Probabilities, Odds, and Expectations: Measuring Uncertainty and Risk40 Questions
Exam 17: The Mathematics of Normality: the Call of the Bell40 Questions
Select questions type
How many different spanning trees can be found in the following network? 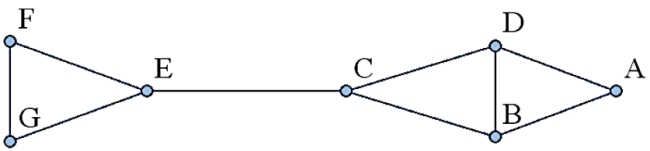
(Short Answer)
4.7/5  (37)
(37)
Is it possible to have a tree in which every vertex has even degree? Explain.
(Essay)
4.7/5  (34)
(34)
The local town board has authorized the creation of a new sub-division consisting of five houses. The public works department is given the duty of installing underground electric wires which will network together the houses with a nearby electric sub-station . The table below gives the coast in hundreds dollars of installing wires between each of the houses and sub-station . Find the coast og the cheapest network connecting the five houses with the sub-station.
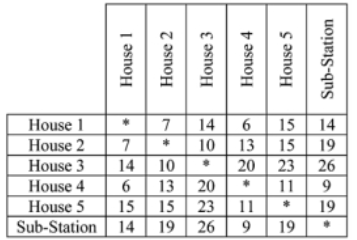
(Multiple Choice)
4.9/5  (37)
(37)
Consider the network shown below; draw two different spanning trees for the network. 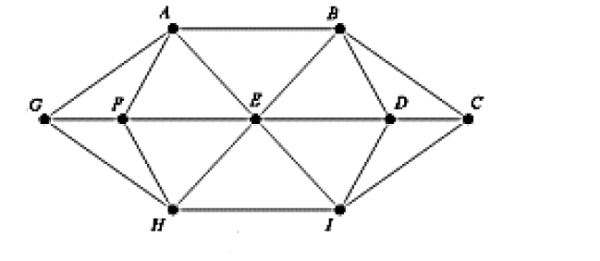
(Essay)
4.7/5  (33)
(33)
A connected graph contains 25 edges and every edge in the graph is a bridge. How many vertices does
the graph contain?
(Short Answer)
4.8/5  (36)
(36)
What number of edges will be bridges in a tree which has fifteen vertices?
(Short Answer)
4.9/5  (38)
(38)
A city consists of five boroughs, and each borough has four neighborhoods and each neighborhood consists of ten houses. You have been hired to run a fiber-optic cable, networking all of the houses to each other. No matter the length, it costs $50 to connect any one house to any other house. Based on all of this information, what will it cost to network all of the houses together so that there are no redundancies? Hint: Think of each house as a vertex.
(Multiple Choice)
4.9/5  (41)
(41)
Consider the network shown below; what is the redundancy of the network? 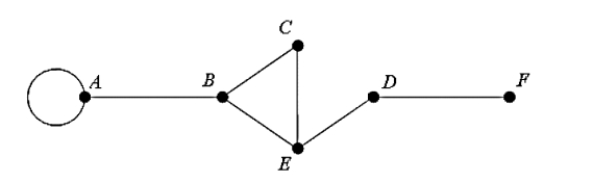
(Short Answer)
4.8/5  (35)
(35)
Which of the following scenarios results in a graph which is not a tree?
(Multiple Choice)
4.8/5  (40)
(40)
Consider the network shown below; draw the minimum spanning tree for this network by applying Kruskal's algorithm. 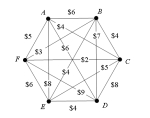
(Essay)
4.8/5  (30)
(30)
The local town board has authorized the creation of a new sub-division of five houses. The public works department is given the duty of installing underground electric wires which will network together the houses with the nearby electric sub-station. The table below gives the cost in hundreds dollars of installing wires between each of the houses and the sub-station. Find the cost of the cheapest network connecting the five houses with the sub-station. 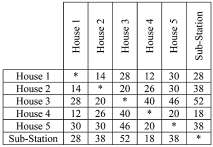
(Multiple Choice)
4.7/5  (37)
(37)
Consider the graph shown below; what is the weight of the minimum spanning tree of the graph?
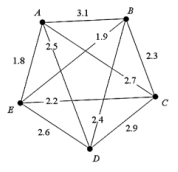
(Multiple Choice)
4.9/5  (32)
(32)
A city consists of four boroughs, and each borough has six neighborhoods and each neighborhood consists of twenty houses. You have been hired to run a fiber-optic cable, networking all of the houses to each other. No matter the length, it costs $75 to connect any one house to any other house. Based on all of this information, what will it cost to network all of the houses together so that there are no
redundancies? Hint: Think of each house as a vertex.
(Short Answer)
4.8/5  (49)
(49)
Consider Graph K shown below; which of the figures shown below are not spanning trees of Graph K?
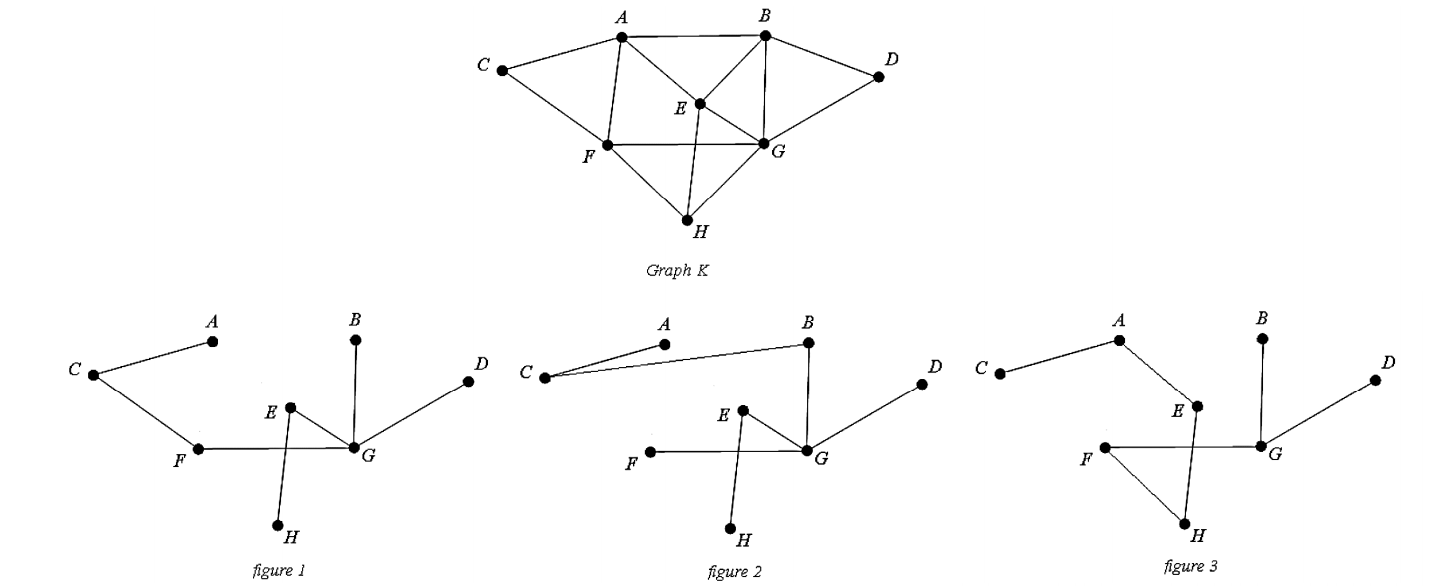
(Multiple Choice)
4.8/5  (39)
(39)
Which of the following scenarios results in a graph which is a tree?
(Multiple Choice)
4.9/5  (34)
(34)
Consider the network shown in problem 4; how many edges are not bridges?
(Short Answer)
4.8/5  (39)
(39)
A city consists of three boroughs, and each borough has five neighborhoods and each neighborhood consists of ten houses. You have been hired to run a fiber-optic cable, networking all of the houses to each other. No matter the length, it costs $100 to connect any one house to any other house. Based on all of this information, what will it cost to network all of the houses in the city together so that there are
no redundancies? Hint: Think of each house as a vertex.
(Short Answer)
4.8/5  (39)
(39)
Showing 21 - 40 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)