Exam 13: Inference in Linear Models
Exam 1: Basic Ideas39 Questions
Exam 2: Graphical Summaries of Data40 Questions
Exam 3: Numerical Summaries of Data76 Questions
Exam 4: Summarizing Bivariate Data33 Questions
Exam 5: Probability99 Questions
Exam 6: Discrete Probability Distributions76 Questions
Exam 7: The Normal Distribution131 Questions
Exam 8: Confidence Intervals62 Questions
Exam 9: Hypothesis Testing115 Questions
Exam 10: Two-Sample Confidence Intervals44 Questions
Exam 11: Two-Sample Hypothesis Tests43 Questions
Exam 12: Tests With Qualitative Data26 Questions
Exam 13: Inference in Linear Models51 Questions
Exam 14: Analysis of Variance48 Questions
Exam 15: Nonparametric Statistics27 Questions
Select questions type
Use the given set of points to compute the residual standard deviation . x 12 20 19 17 19 10 y 43 69 65 58 64 36 x=13
(Multiple Choice)
4.8/5  (45)
(45)
Use the given set of points to construct a prediction interval for an individual response for the given value of .
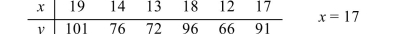
(Multiple Choice)
4.8/5  (35)
(35)
The following MINITAB output presents a multiple regression equation .
The regression equation is
Predictor Coef SE Coef T P Constant 3.9695 0.8785 0.9299 0.327 X1 1.4577 0.6034 3.5107 0.003 X2 -1.7859 0.7302 -3.1148 0.005 X3 0.7686 0.6732 1.9294 0.088 X4 0.0777 0.7569 -1.0782 0.352
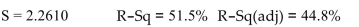 Source DF SS MS F P Regression 4 1,148.7 287.2 9.0031 0.003 Residual Error 34 1,083.9 31.9 Total 38 2,232.6
Is the model useful for prediction? Use the = 0.05 level.
Source DF SS MS F P Regression 4 1,148.7 287.2 9.0031 0.003 Residual Error 34 1,083.9 31.9 Total 38 2,232.6
Is the model useful for prediction? Use the = 0.05 level.
(True/False)
4.8/5  (35)
(35)
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 8 subjects. Times were measured in thousandths Of a second. The results are presented in the following table.
Visual Auditory 193 189 240 222 239 226 236 225 200 189 161 158 214 209 204 193
Construct a 95% confidence interval for the slope of the least-squares regression line.
(Multiple Choice)
4.9/5  (38)
(38)
Use the given set of points to test the null hypothesis level of significance.
x 14 7 15 10 9 6 14 15 y 32 17 36 26 21 15 34 37
(Multiple Choice)
4.9/5  (40)
(40)
The following MINITAB output presents a confidence interval for a mean response and a prediction
interval for an individual response. New Obs Fit SE Fit 95.0\% CI 95.0\% PI 1 9.582 1.189 (3.264,15.900) (2.795,16.369) Values of Predictors for New Observations New Obs X1 X2 X3 1 1.94 1.11 1.17 What is the 95% confidence interval for the mean response?
(Short Answer)
5.0/5  (41)
(41)
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 8 subjects. Times were measured in thousandths of A second. The results are presented in the following table.
Visual Auditory 249 246 194 241 210 244 197 245 208 243 166 243 239 252 151 242
Construct a 95% prediction interval for the auditory response time for a particular subject whose Visual response time is 182.
(Multiple Choice)
4.8/5  (38)
(38)
Use the given set of points to compute . x 11 5 7 6 9 8 14 12 y 24 17 19 20 23 17 30 25
(Multiple Choice)
4.9/5  (45)
(45)
The following MINITAB output presents a 95% confidence interval for the mean ozone level on days when the relative humidity is 40%, and a 95% prediction interval for the ozone level on a Particular day when the relative humidity is 40%. The units of ozone are parts per billion. Predicted Values for New Observations
New Obs Fit SE Fit 95.0\% CI 95.0\% PI 1 44.17 1.5 (41.23,47.11) (28.00,60.34)
Values of Predictors for New Observations
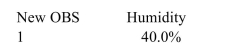 What is the confidence interval for the mean ozone level for days when the relative humidity is ?
What is the confidence interval for the mean ozone level for days when the relative humidity is ?
(Multiple Choice)
4.7/5  (46)
(46)
Use the given set of points to compute the sum of squares for x,(x- . x 5 9 10 7 7 10 6 8 y 16 22 27 20 21 22 20 21
(Multiple Choice)
4.8/5  (35)
(35)
In a study of reaction times, the time to respond to a visual stimulus (x) and the time to respond to an auditory stimulus (y) were recorded for each of 8 subjects. Times were measured in thousandths of a second. The results are presented in the following table.
Visual Auditory 168 245 171 242 185 240 235 249 171 239 182 246 173 240 249 246
i). Compute the least-squares regression line for predicting auditory response time (y) from visual res time (x).
ii). Construct a 99% confidence interval for the slope of the least-squares regression line.
iii). Test H0: =0 versus .Use the =0.01 level of significance.
(Short Answer)
4.9/5  (41)
(41)
Showing 41 - 51 of 51
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)